dy/dx + (-sinx)y=2sinx

Question

Solution of first order differential equations (DEs) by Method of integrating factors, verification and graph of solution via MATLAB 

Question 1: For the following first order initial value problems,

 i. State the nature of given DE (linear / nonlinear / homogeneous / nonhomogeneous).

 ii. Find solution (by hand) by method of integrating factors and via MATLAB as well.

 iii. Give verification of solution by hand as well as via MATLAB. 

iv. Give all the largest intervals of solution where the solution is differentiable.

 v. Determine whether there are any transient terms in the solution (lim 0 x→ (transient term) = ). 

vi. Plot the solution via MATLAB over any piece of interval of solution or domain of solution.

Answer 1

This is an example of a first order differential equation. To solve it we need to find an integrating factor so that the left-hand side becomes an easily integrable expression. 

This is achieved in this case by calculating e^∫-sin(x)dx=e^cos(x) which becomes the integrating factor:

e^cos(x)dy/dx-sin(x)e^cos(x)y=2sin(x)e^cos(x),

(d/dx)(e^cos(x)y)=2sin(x)e^cos(x),

ye^cos(x)=2∫sin(x)e^cos(x)dx=-2e^cos(x)+C where C is the constant of integration.

Therefore y=-2+Ce^-cos(x).

CHECK:

y=-2+Ce^-cos(x), so Ce^-cos(x)=y+2

dy/dx=-Csin(x)e^-cos(x)=ysin(x)+2sin(x),

dy/dx-ysin(x)=2sin(x)✔️

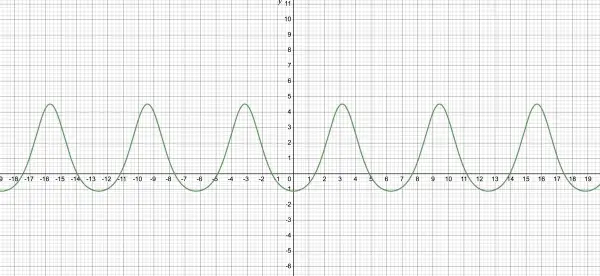
-1≤cos(x)≤1 no matter what size x is, so e^-cos(x) can only lie between 1/e and e, which are not transient values. The appearance of y when graphed is a series of waves (like sine) with fixed amplitude and period. The constant C determines the magnitude of the amplitude. When C=0, y=-2, a flat line, of course. On either side of C=0, the wave pattern is largely below or above the x-axis. The function is continuous, and is also continuously differentiable, the interval being (-∞,∞).

I don't have access to MATLAB, but I hope my solution helps. Here is a graph using a positive value of C:

Picture by courtesy of Desmos.com/calculator

As C shrinks to zero the graph shrinks to the line y=-2.