In the trapezoid ABCD ( AB ∥ CD ) point M∈ AD , so that AM:MD=3:5. Line l ∥ AB and going trough point M intersects diagonal AC and leg BC at points P and N respectively. Find: BC:BN

Question

You have to use thales theorem, thales corollay, and their converses as well as find the ratio using them. Please give statement/reasoning proof

Answer 1

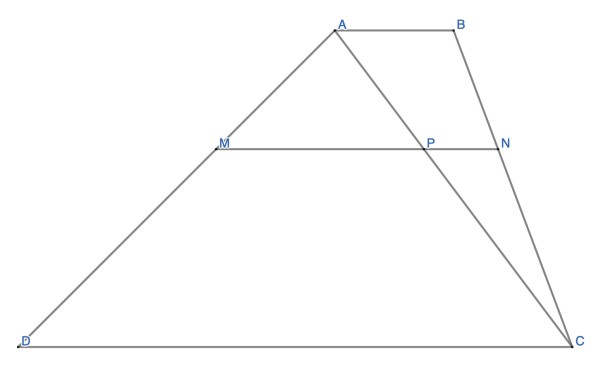
The diagonal splits the trapezoid into two triangles ACD and ABC.

MN creates two pairs of similar triangles: AMP and ACD, and CNP and ABC.

Thales' Theorem (one of several) concerns the proportionality of the sides of similar triangles. Applying it, we get:

Let AD=8x, then AM=3x and DM=5x, AD=8x, because AM/AD=3/8=AP/AC (Thales);

let AC=8y, then AP=3y and CP=5y, because of similar triangles AMP and ACD.

CP/AC=5/8=CN/BC, because of similar triangles CNP and ABC.

If BC=8z, then CN=5z and BN=3z, making BC/BN=8/3, or BC:BN=8:3.

The corollary to this is that a line (l in this case) parallel to the parallel sides of a trapezoid, creating two similar trapezoids, also creates equal proportionalities in the sloping sides, because the diagonal divides the trapezoid into two triangles which are not generally similar but nevertheless share corresponding proportionalities: AM:MD=BN:NC, for example.