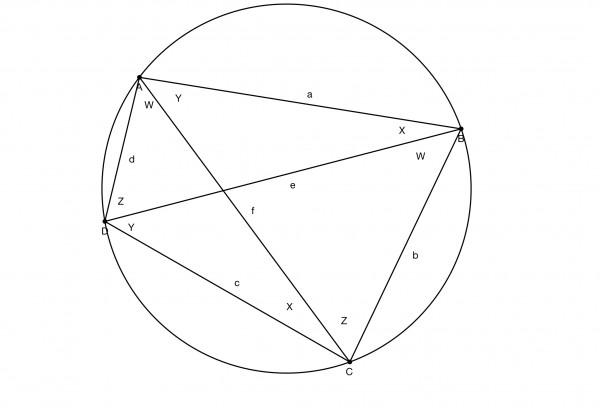
The picture shows a cyclic quadrilateral ABCD, with four chords, CD (c), AD (d), BC (b) and AB (a). Angle CAD=CBD=W, ABD=ACD=X, CDB=CAB=Y, and ADB=ACB=Z (angles in the same segment, subtended by the same chord, are equal).
The diagonals AC and BD are respectively labelled f and e.
Also, for general angle x, sin(x)=sin(180-x).
W+X+Y+Z=180; let P=sin(W+Y)=sin(X+Z), let Q=sin(Y+Z)=sin(X+W).
By the sine rule, f/sin(X+W)=b/sinY, so f=bsin(X+W)/sinY=bQ/sinY=dsin(Y+Z)/sinX=dQ/sinX.
Similarly, e=bsin(X+Z)/sinY=bP/sinY=dsin(W+Y)/sinX=dP/sinX.
Therefore, f/e=(dQ/sinX)/(dP/sinX)=Q/P.
Area of a triangle=½(product of two sides)(sine of the angle between them):
Area of ∆ABD=½adsin(W+Y); area of ∆ABC=½absin(W+X);
area of ∆BCD=½bcsin(X+Z); area of ∆ACD=½cdsin(Y+Z).
Area ∆ABD+∆BCD=½adsin(W+Y)+½bcsin(X+Z)=½(ad+bc)P because sin(X+Z)=sin(W+Y)=P.
Area ∆ABC+∆ACD=½absin(W+X)+½cdsin(Y+Z)=½(ab+cd)Q.
But Q/P=f/e, so Q=Pf/e.
Area of ABCD=area of ∆ABD+∆BCD=area of ∆ABC+∆ACD.
So, ½(ad+bc)P=½(ab+cd)Q=½(ab+cd)Pf/e.
Therefore, f(ab+cd)=e(ad+bc) or AC(AB.BC+CD.DA)=BD(AB.AD+BC.CD) QED.