The university wants to build a tennis court an equal distance from all three residences located at points A(2,2), B(10,6), and C(4,8) . Determine the coordinates of the tennis court

Question

A university has 3 student residences, which are located at points A(2,2), B(10,6), and C(4,8) on a grid. The university wants to build a tennis court an equal distance from all three residences. Determine the coordinates of the tennis court

Answer 1

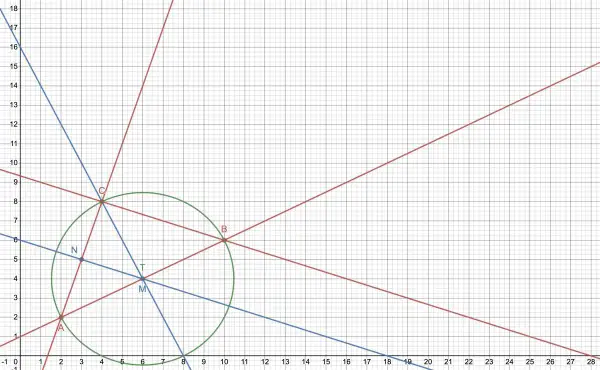
The circumscribed circle of the triangle ABC has centre T, where AT=BT=CT are radii. To construct this circle we need the midpoints of AB, AC and BC=M(6,4), N(3,5), P(7,7). The midpoints are the averages of the x and y coordinates of pairs of vertices. However, we don't them all, so we'll just use M and N. The intersection of all the perpendiculars will be T, and the perpendicular on P is bound to intersect the other perpendiculars at T.

The slope of AB=(6-2)/(10-2)=4/8=½; slope of AC=(8-2)/(4-2)=6/2=3.

The corresponding slopes of the perpendiculars are -2 and -⅓, because the product of the slopes has to be -1.

From the slopes and midpoints we can find the equations of the perpendiculars.

MT is y-4=-2(x-6), NT is y-5=-(x-3)/3 in slope intercept form. So when they intercept:

4-2(x-6)=5-(x-3)/3 because the y coords are the same.

12-6(x-6)=15-(x-3),

12-6x+36=15-x+3,

48-18=5x, x=6⇒y=4. So T=(6,4). This happens to be the point M, so AB is a diameter and vertex C is a right angle.