What is the ratio of two radii r/R?

Question

Two circles of different sizes intersect to form an Area, A1. The larger circle has a radius of R
The smaller circle have a radius of r and an area of A2.
The ratio between the two areas is:

A1/A2=0.5

Given this information what is the ratio between the the two radii:

r/R=?

Answer 1

A2=πr², A1/A2=0.5=½ (given), so A1=½πr². Let p=r/R, the ratio to be found, then r=pR and A1=½πp²R².

Let the centre of the larger circle be O₁ and that of the smaller circle O₂. Let the line segment O₁O₂=a (the separation of the centres of the circles). Let the circles intersect at common points A and B on both circles. O₁A=O₁B=R, O₂A=O₂B=r=pR. Join A to B, then chord AB, common to both circles, is perpendicular to O₁O₂ and AB splits the area A1 into two parts A1_R and A1_L, where L and R indicate left and right parts of A1. Let AB subtend angle θ₁ in the larger circle and θ₂ in the smaller circle, then a=Rcos(½θ₁)+rcos(½θ₂).

The area A1 can be expressed as the sum of the differences in area between a circular segment and an isosceles triangle in each circle.

For the larger circle: A1_R=½(R²θ₁-R²sin(θ₁))=½R²(θ₁-sin(θ₁)) (that is, segment area minus triangular area)

For the smaller circle: A1_L=½(r²θ₂-r²sin(θ₂))=½p²R²(θ₂-sin(θ₂)).

So A1=½πp²R²=½R²(θ₁-sin(θ₁))+½p²R²(θ₂-sin(θ₂))=½R²(θ₁-sin(θ₁)+p²(θ₂-sin(θ₂))),

πp²=θ₁-sin(θ₁)+p²(θ₂-sin(θ₂)), π=(θ₁-sin(θ₁))/p²+θ₂-sin(θ₂), by dividing through by ½R² and then by p².

O₁O₂ bisects θ₁ and θ₂. AB is a common chord and also the common base of two isosceles triangles.

AB=2Rsin(θ₁/2)=2rsin(θ₂/2), p=r/R=sin(θ₁/2)/sin(θ₂/2), from which it's clear that, since R>r (p<1), θ₂>θ₁.

p²=sin²(θ₁/2)/sin²(θ₂/2), or, using the identity cos(2A)=1-2sin²(A), that is, sin²(A)=½(1-cos(2A)), and substituting A=½θ₁ and A=½θ₂:

p²=(1-cos(θ₁))/(1-cos(θ₂)). Therefore:

π=(θ₁-sin(θ₁))(1-cos(θ₂))/(1-cos(θ₁))+θ₂-sin(θ₂).

This equation contains two variables so there is no unique solution for θ₁ and θ₂, implying that there is no unique solution for r/R.

EXAMPLE

The picture below illustrates the example.

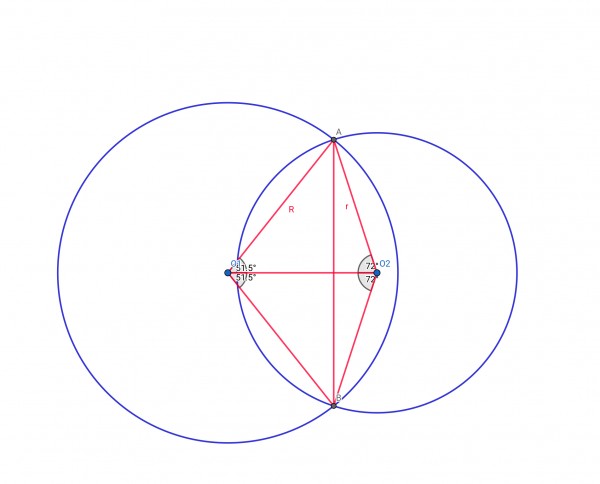
Let θ₁=1.7980 radians (103° approx) and θ₂=0.8π (144°), then p=r/R=0.823 approx. There are many solutions: if the small circle is reduced in size without reducing the large circle, then it's easy to see that, by adjusting the distance between the centres of the circles, the large circle can be made to cover exactly half the area of the small circle. This changes the sizes of the angles in the triangles and r/R also changes, hence many solutions.