dy/dx=(dy/dt)/(dx/dt)=0 when t=1.
Also dx/dt≠0 for all t, and dy/dx can never be infinite (vertical), so let dx/dt=k, a constant.
Therefore x=kt+c₁ where c₁ is a constant.
When t=-2, x=f(t)=4, so:
4=-2k+c₁, c₁=2k+4.
Since dy/dx=0 when t=1, dy/dt=0.
If dy/dt=a(t-1) where a is a constant then:
y=g(t)=at²/2-at+c₂, where c₂ is a constant.
When t=-2, y=5, so:
5=2a+2a+c₂, c₂=5-4a.
Therefore f(t)=kt+2k+4, g(t)=at²/2-at+5-4a.
Since a and k are arbitrary, let a=2 and k=1.
So a solution is f(t)=t+6, g(t)=t²-2t-3.
Range of f is determined by f(-2)=4 and f(5)=11 (linear).
Range of g is determined by g(-2)=5 and g(5)=12 (quadratic).
Since x=t+6, t=x-6, so y=(x-6)²-2(x-6)-3=x²-14x+45, with range [-4,12].
dy/dx=0 when t=1, that is at the point (1+6,1-2-3)=(7,-4).
CHECK
f(-2)=4, g(-2)=5 producing the point (4,5).
df/dt=1, dg/dt=2t-2=0 when t=1 (horizontal tangent).
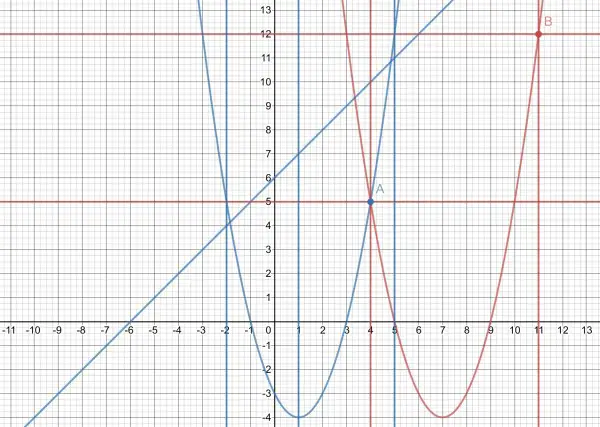
The blue sloping line is f(t)=t+6 and the blue parabola is g(t)=t²-2t-3, vertex at (1,-4). The blue vertical lines determine and enclose -2≤t≤5, the domain of t and t=1 (for minimum gradient of y).
The red parabola is y=x²-14x+45, vertex at (7,-4). The red verticals determine and enclose 4≤x≤11, and the red horizontals determine and enclose 5≤y≤12. These correspond to the domain of t. A(4,5) and B(11,12) show the lower and upper limits of the parabola as determined by the domain of t.