We need the Z score for each of the grade conditions.
Z=(X-µ)/σ gives the relevant Z score. Let’s apply this formula for each grade where X=x. Ignore the inequality for the time being and just use equality. We can come back to the inequality later.
A: x=µ+σ, Z=(µ+σ-µ)/σ=1, P(Z=1)=0.8413.
B: x=µ+σ and x=µ, Z₁=1, P₁(Z₁=1)=0.8413 and Z₂=0, P₂(Z₂=0)=0.5.
C: x=µ-σ and x=µ, Z₁=(µ-σ-µ)/σ=-1, P₁(Z₁=-1)=1-P(Z=1)=1-0.8413=0.1587, P₂(Z₂=0)=0.5.
D: x=µ-2σ and x=µ-σ, Z₁=(µ-2σ-µ)/σ=-2, P₁(Z₁=-2)=1-P(Z=2)=1-0.9772=0.0228, P₂(Z₂=-1)=0.1587.
F: x=µ-2σ, P(Z=-2)=0.0228.
Now, let’s analyse what we just did.
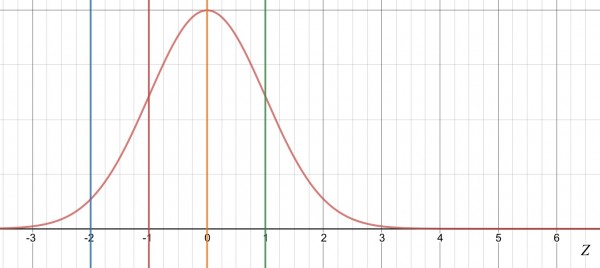
Here’s the nice bit—a picture.
The red bell-shaped curve is the normal distribution. The vertical lines represent the Z scores for the grades, or, rather, the cutoff or critical values that separate the grades, because a grade is a band (determined by the inequalities in the question). The area under the red curve to the right of the green line is the grade A band; the area between the amber and green lines is the grade B band; the area between the red and amber lines is the grade C band; and the the area between the blue and red lines is the grade D band. The area to the left of the blue band is all grade F.
It should now be getting clear what to do next. The total area under the curve is 100% of all the results, so we can see that each grade band is a fraction of this area, that is, some percentage. Normal distribution tables give the area under the curve to the the left (that is, less than) a specific Z score.
For grade A we need the area to the right, so we can get this in two ways. Look up Z=1 to get the area to the left, then subtract this from 1 (or 100%) to get the area to the right. The other way makes use of symmetry. The area to the left of Z=-1 has the same size as the area to the right of Z=1. So the band for grade A is 1-0.8413=0.1587 or 15.87%.
Note that the amber line splits the distribution in half exactly, and corresponds to 0.5 or 50% of the results. We know the area to the left of the green line is 0.8413 and the area to the left of the amber line is 0.5. So the area in between is 0.8413-0.5=0.3413 or 34.13%. Grade B is therefore about 34%.
Grade C band is the mirror of grade B band, so must also be 34%.
We know that the area to the left of the red line is the same size as the area to the right of the green line, 0.1587. This is the upper limit for the grade D band. The lower limit is when Z=-2, corresponding to 0.0228. The difference between these is 0.1587-0.0228=0.1359 or 13.59%, and this is the percentage for grade D.
Grade F is to the left of the blue line at Z=-2, and consists of 0.0228 or 2.28% of the results.
I hope this detailed explanation helps you to understand how to solve this type of problem.