First thing I noticed about this question was that it involved sine and cosine functions. A mental picture of what they look like came to mind: the sine function (red) and the cosine function (green) are waves that repeat (cycle) all along the x-axis.
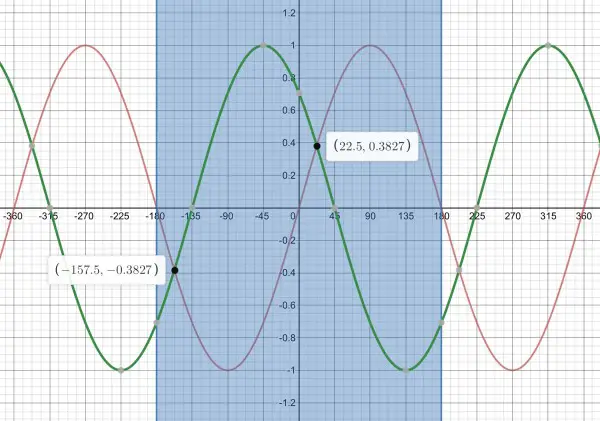
You can see an example below of how they intersect. The blue shaded area represents -180≤x≤180 the region we’re interested in. This example is in fact the whole of this problem including its solution. It helps a lot to have a picture, because it turns the abstract maths into something you can see and study.
In this picture, p is a phase displacement (sideways movement) and q represents amplitude (maximum height and depth). But how do we work out p and q (question 1). The answer is we can’t unless we first understand the information in question 2. An intersection point is the graphical solution of f(x)=g(x), that is, when cos(p+x)=qsin(x). We know x=22.5º and f(x)=g(x)=0.38, and because these functions are drawn on the same graph, they are both y. There’s a red y and a green y, and they have the same value at the intersections (the black dots).
We find q first because we know that g(x)=qsin(22.5) (which you would probably write as qsin(22,5))=0.38 (0,38), so q=0.38/sin(22.5)=0.38/0.3827=0.993. I think you’re expected to round this up to 1. So q=1. We also know that f(22.5)=cos(22.5+p)=0.38.
So we need cos⁻¹(0.38)=45.17º approximately, and I think you’re expected to round this up to p=45º. Hence f(x)=cos(x+45),g(x)=sin(x).
(2) To solve this (that is, find the intersection points), we use the fact that sin(x)=cos(90-x), so when f(x)=g(x), cos(x+45)=cos(90-x), therefore x+45=90-x, 2x=90-45=45, x=45/2=22.5º. We already knew that, because it’s point A(22.5,0.38) (or A(22,5;0,38)). This is where the graph helps. Because of symmetry, point B (the other black dot) is as far below the x-axis as A is above, so the y-coordinate is -0.38, and sin⁻¹(-0.38)=-22.5º. But (-22.5,-0.38) is on the red curve (g(x)) but not on the green curve (f(x)). We need to move to the left to get to the black dot representing B, inside the blue shading. The point (-22.5,-0.38) is displaced 22.5º to the left of the y-axis and, by symmetry, point B is displaced 22.5º to the right of -180º, so the x-coordinate is -180+22.5=-157.5º. So B is (-157.5,-0.38). There are other ways you can work this out from the graph, and that’s why it’s useful to have a picture.
(3) f(x)-g(x)=0 when f(x)=g(x), which gives the intersection points in which x=22.5 and -157.5, the difference between these points is 22.5-(-157.5)=22.5+157.5=180º, the interval between the x solutions of f(x)-g(x)=0.
4a) f(x) is shifted 30º left to become h(x)=cos(x+75).
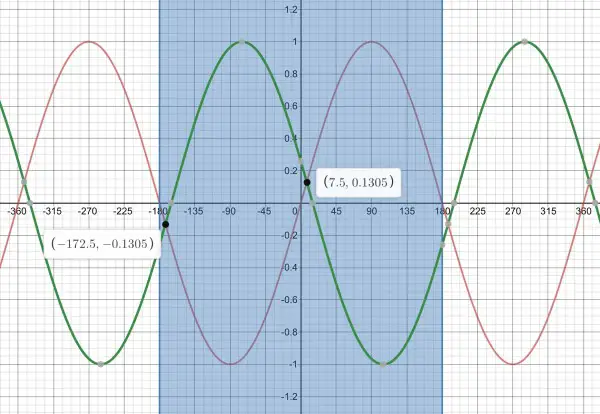
4b) If I understand correctly what you’re asking, this changes the intersection points, and we solve for x:
x+75=90-x, 2x=90-75=15, x=7.5º and h(7.5)=0.13 approx. So the point is (7.5,0.13) and the other point is (-180+7.5,-0.13)=(-172.5,-0.13). The difference between the x coordinates is again 180º.