Given f(x) = - x^2 +2x +3 and g(x) = 1-2^x

Question

1) for which values of x if f(x)×g(x) >or eqaul to 0. 2) Determine the value of c such that the x-axis will be tangent to the graph of h where h(x)=f(x) +c

Answer 1

(1) The product is zero when any of the factors are zero.

So 1-2ˣ=0 when 2ˣ=1, and x=0.

When -x²+2x+3=-(x²-2x-3)=-(x-3)(x+1)=0, x=3 or -1.

So we have three possible (critical) values for x: -1, 0, 3, therefore we consider the sign of f and g in 4 intervals: x<-1, x in (-1,0), x in (0,3) and x>3:

x<-1: f(x)<0, g(x)>0, f(x)g(x)<0;

x in (-1,0): f(x)>0, g(x)>0, f(x)g(x)>0;

x in (0,3): f(x)>0, g(x)<0, f(x)g(x)<0;

x>3: f(x)<0, g(x)<0, f(x)g(x)>0.

So f(x)g(x)≥0 when x=-1, x in (-1,0), x=0, x=3, x>3.

This can be summarised: -1≤x≤0, x≥3.

In words: x is between -1 and zero inclusive, or x is greater than or equal to 3.

(2) h(x)=f(x)+c=-x²+2x+3+c. The x-axis is h(x)=0, so:

h(x)=-x²+2x+3+c is a parabola (inverted U shape).

The equation can be h(x)=-(x²-2x-3-c)=-(x²-2x+1-4-c),

Let y=h(x)=-(x-1)²+4+c, y-(4+c)=-(x-1)².

The vertex (maximum in this case) is at (1,4+c). The vertex must lie on the x-axis (y=0) so 4+c=0 and c=-4.

h(x)=-x²+2x-1 or -(x-1)².

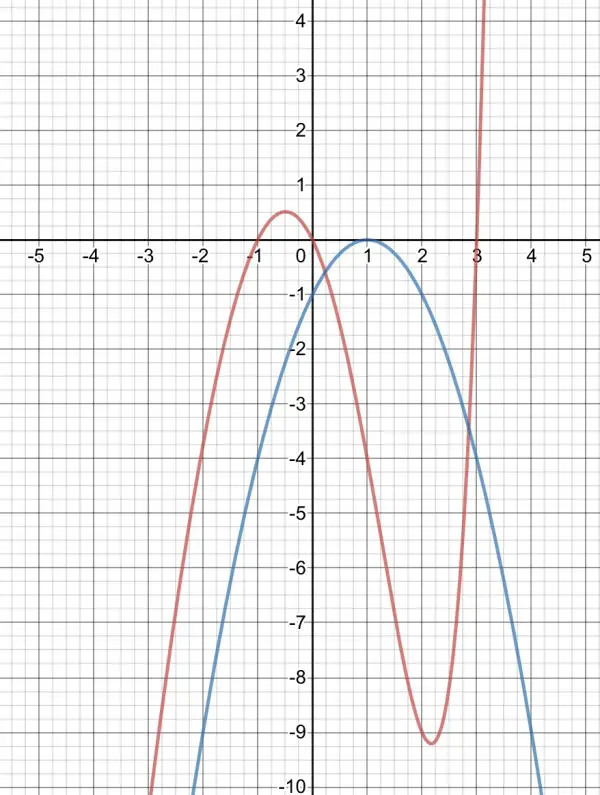
Red=f(x)×g(x), blue=h(x).