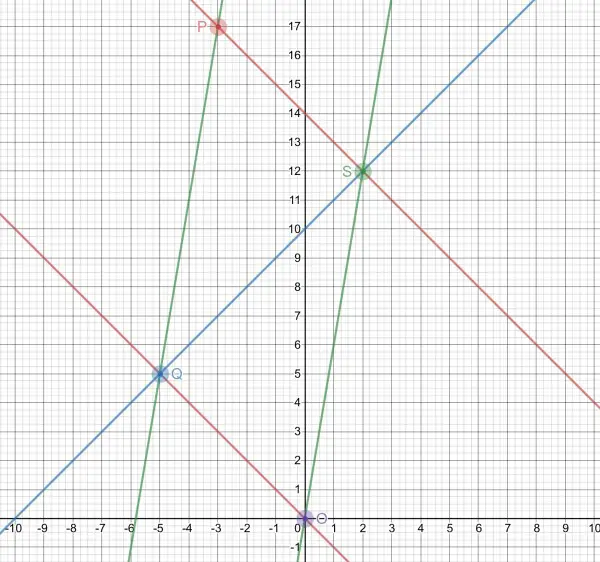
(1) QP is parallel to OS so it has the same gradient=6.
Use the point-slope form of the line equation first because the line passes through P(-3,17):
y-17=6(x+3)=6x+18, so y=6x+35 is the equation of QP.
(2) The coordinates of Q are where OQ and QP meet:
y=-x=6x+35, so 7x=-35, x=-5 and y=-x=5. So Q(-5,5).
(3) Using Pythagoras on the right triangle formed by the perpendicular from Q to the x-axis=y coordinate=5, where OQ is the hypotenuse and the other leg is the magnitude of the x coordinate=5, we have OQ=√(5²+5²)=5√2 units (=7.07 units approx).
(4) The angle between QO and the negative x-axis is 45º (arctan(5/5)=arctan(1)). The tangent of the angle between OS and the positive x-axis is 6, the slope of OS. So since ∠QOS is between these two angles we know that they add up to 180º. ∠QOS=180-45-arctan(6)=135-arctan(6)=54.46º approx.
(5) OS=√(12²+2²)=√148 (also given). The equation of PS is:
y-17=-(x+3), y=14-x. The coordinates of S are the solution of y=6x=14-x, 7x=14, x=2, y=6x=12, giving S(2,12), hence OS=√148. QS is the hypotenuse of a right triangle with leg lengths 2-(-5)=7 (horizontal), 12-5=7 (vertical). QS=√(7²+7²)=7√2=9.90 units approx.