Circle is tangent to y-axis. The center is on line x − 3y = 0. Line y = x intersects with the circle at two points A and B. The length of AB is 2sqrt(27). Find the equation of the circle.

Question

I played around with desmos and got that these two equations work:
(x-3)^2+(y-1)^2=9,(x+3)^2+(y+1)^2=9

I'm not sure how to get here in a systematic way with equations and that's what I'm looking for.
 

Comments

I think there’s an error. The length of AB should be 2sqrt(7) not 2sqrt(27). This confirms what you discovered using Desmos. 2sqrt(27) is much too large.

Answer 1

 

If the circle’s centre is at (h,k) then this point must lie on x-3y=0, therefore h=3k. Because the y-axis (x=0) is a tangent the radius=3k. We can therefore write the equation of the circle in terms of k:

(x-3k)²+(y-k)²=9k²

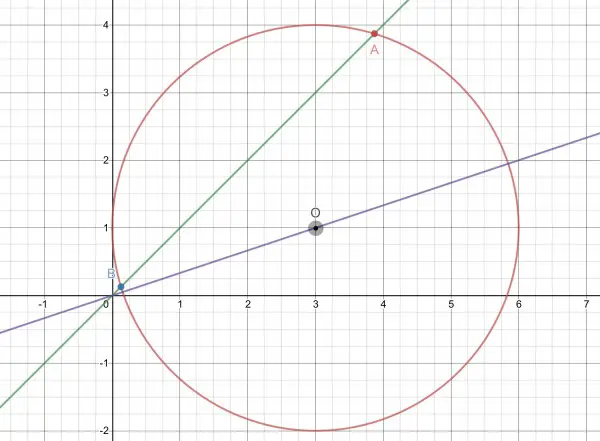
The line y=x intersects the circle at A and B.

We need to solve for x:

(x-3k)²+(x-k)²=9k²,

x²-6kx+9k²+x²-2kx+k²=9k²,

x²-4kx=-k²/2,

x²-4kx+4k²=4k²-k²/2=7k²/2,

(x-2k)²=7k²/2,

x-2k=±k√(7/2)=±k√14/2. The y values are the same because y=x.

So let A=(2k+k√14/2,2k+k√14/2) and B=(2k-k√14/2,2k-k√14/2)

To find the length of AB we use Pythagoras:

√(14k²+14k²)=√(28k²)=2k√7=2√27, and k=√(27/7).

I suspect that AB=2√7, which would make k=1.

The equation would then be (x-3)²+(y-1)²=9.

This can also be written:

x²-6x+y²-2y+1=0.

This makes A=(2+√14/2,2+√14/2) and B=(2-√14/2,2-√14/2).

See picture.