In this question I explore the relationship between integration and summation: Integration is a summation of infinitesimal areas (of width dx) while ∑ is summation of discrete areas of a discrete unit width (defined by integer n). But the principle of summation is the same. What I hope to show is that the given summation and the area under a curve are connected so that the summation is in fact an approximation of the area under the curve given by y=f(x)=1/(x²+1), so that, knowing the exact area under the curve (which involves π) it’s possible to confine the approximation between limits.
Consider ∫[0,1]dx/(x²+1)=tan⁻¹(x)[0,1]=π/4. ∫[0,∞]dx/(x²+1)=tan⁻¹(x)[0,∞]=π/2.
∫[0,∞]dx/(1+x²)=∫[0,1]dx/(1+x²)+∫[1,∞]dx/(1+x²)=π/4+π/4=π/2. The square brackets indicate an interval [low,high] for the integration.
Note that when x=0, y=1/(x²+1)=1, x=1, y=½ (A on the graph below), x=2, y=⅕ (B on the graph), x=3, y=¹⁄₁₀ (not shown on the graph).
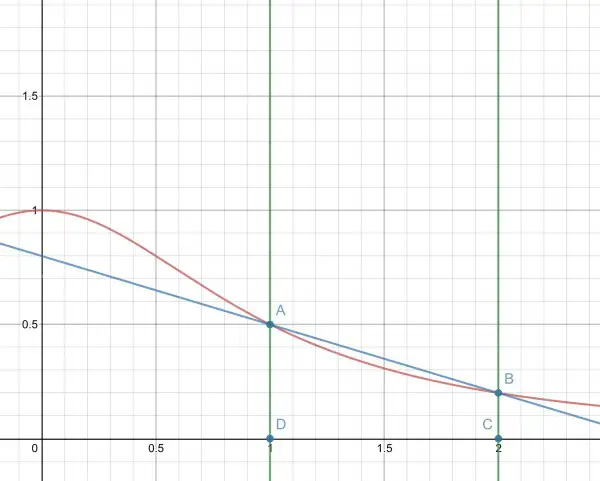
In the graph above, the red curve is the function 1/(x²+1). From the above integrations the area between the curve and the asymptotic x-axis comes out as π/2 (actually, the area approaches π/2, because the curve never quite touches the x-axis), while the area between the curve, the axes and the line AD is π/4, making the area under the curve to the right of AD also π/4. The small grid squares have side 0.1 units so that you can check out the areas by counting the squares.
We can calculate the area of trapezoid ABCD knowing A(1,½) and B(2,⅕):
½(½+⅕)(2-1)=7/20=0.35. We can also calculate two rectangular areas: AD×DC=0.5 (“exterior” rectangle) and BC×DC=0.2 (“interior” rectangle). These rectangles enclose the curve. A trapezoid can be similarly constructed adjacent to ABCD, say, BEFC with area ½(⅕+¹⁄₁₀). The total area of ABCD and BEFC=½(½+⅕+⅕+¹⁄₁₀)=½(½+¹⁄₁₀)+⅕. Adding in the area of the next trapezoid we get ½(½+¹⁄₁₇)+⅕+¹⁄₁₀, and so on.
Note that this is beginning to look like ∑1/(n²+1). As we add together the areas of the trapezoids it begins to look like ¼+∑[2,∞]1/(n²+1). And we know that this sum approximates to the area under the curve=π/4.
The area sum can be written ¼-½+∑[1,∞]1/(n²+1)≈π/4, or:
∑[1,∞]1/(n²+1)≈π/4+¼. All I’ve done here is to allow for the first term of the series (=1/(1²+1)) so that we can write in the complete series.
Now let’s get back to the exterior and interior rectangles.
The first exterior rectangle (n=1 to 2) has area ½; the first interior rectangle has area ⅕. In general, this is 1/(n²+1) for the area of the exterior rectangle and 1/((n+1)²+1)=1/(n²+2n+2) for the interior rectangle. The total area of the exterior rectangles is greater than π/4 and the total area of the interior rectangles is less than π/4 because the curve is trapped between the two sets of rectangles.
The sum ER of the areas of the exterior rectangles is 1/2+1/5+1/10+1/17+1/26+... and the sum IR of the areas of the interior rectangles is 1/5+1/10+1/17+1/26+... so IR=ER-½.
ER>π/4 and IR<π/4, so ER-½<π/4, or ER<½+π/4. But ER=∑[1,∞]1/(n²+1),
so π/4<∑[1,∞]1/(n²+1)<½+π/4.
You might ask, what about the trapezoid approximation? As it happens, the approximation can be rewritten:
∑[1,∞]1/(n²+1)>π/4+¼, because the curve has concavity between x and x+1 for x in [1,∞) (concavity actually starts at x=1/√3), so the slant of the trapezoid is always above the curve (see trapezoid ABCD), making the area of the trapezoid greater than the area under the curve. This enables us to improve the answer:
¼+π/4<∑[1,∞]1/(n²+1)<½+π/4.