The Riemann sum gives the definite integral of the function (x-2)3 between the limits [0,4]. The question doesn't specify what increment to use for the width of the rectangles, nor does it specify the left or right Riemann sum.
This function has equal sums above and below the x-axis over the given range. These would cancel out giving a zero result. However, if the integration is performed for the interval [2,4] then doubled, we get the sum of the areas above and beneath the x-axis.
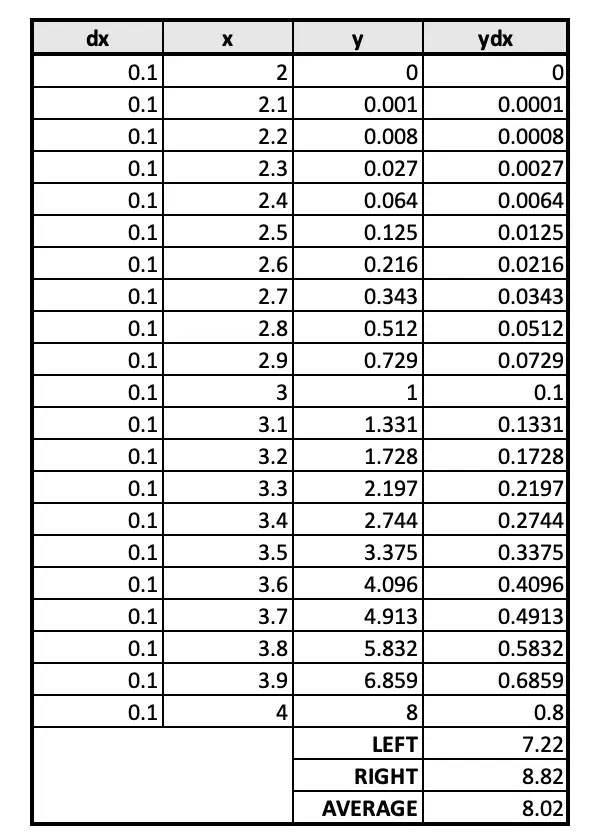
The above table uses an increment of dx=0.1 and computes the left and right Riemann sums. The average of these os close to the actual integral of 8 (the sum of the magnitudes of the areas above and below the x-axis in the interval [0,4]). The definite integral between [0,4]=0 because the areas cancel out.