The denominator factorises: (x-4)(x+3) so the fraction is undefined for x=4 or -3. However, neither x-4 nor x+3 is a factor of the numerator, so solving for x is not going to produce anomalies.
First, reduce the equation to a polynomial by multiplying both sides by the denominator:
2x³-x²+7=23x²-23x-276 which becomes the polynomial:
2x³-24x²+23x+283=0.
Now we draw a rough graph of the polynomial and note that it intersects the x-axis at approximately -3, 6, 9.
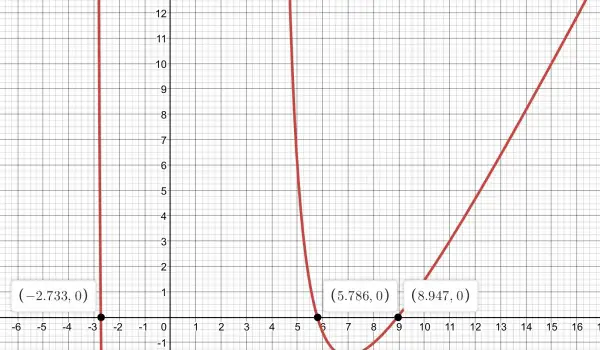
Using Newton’s Method we get the iterative formula:
x=x-(2x³-24x²+23x+283)/(6x²-48x+23), where the denominator here is the derivative of the numerator.
We start with each approximate solution and use the formula iteratively until we get a stable value. Using this method and a 9 decimal place calculator we get:
x=-2.733255918, 5.786296173 or 8.946959745.