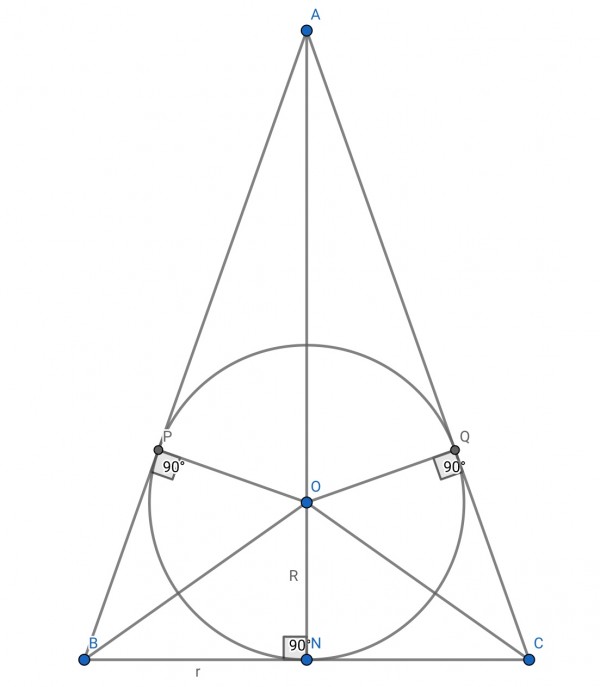
The vertical cross-section of a cone is an isosceles triangle ABC, where the base is BC and A the vertex angle such that ∠ABC=∠ACB. The perpendicular bisector AN from A to BC is also the bisector of angle A. BN=CN=r the radius of the cone.
AN=h, the height of the cone whose volume is πr²h/3. The bisectors of angles B and C meet the bisector of angle A at O, which is the centre of the inscribed circle radius R=OP=OQ=ON. AB and AC are tangents to the circle at P and Q respectively. ∠OPA=∠OQB=90°.
There are 4 congruent triangles: OPB, ONB, OQC, ONC. BP=BN=CN=CQ=r. The inscribed circle is a vertical cross-section of the sphere inside the cone.
h=AN=AO+ON=AO+R, so AO=h-R, and AP²+OP²=AO². Therefore, AP²=(h-R)²-R²=h²-2Rh.
Also, AB=AP+BP=√(h²-2Rh)+r, and AB²=AN²+BN²=h²+r².
Therefore, (√(h²-2Rh)+r)²=h²+r²,
h²-2Rh+r²+2r√(h²-2Rh)=h²+r²,
r√(h²-2Rh)=Rh.
So, squaring both sides:
r²(h²-2Rh)=R²h², r²h-2Rr²=R²h, h(r²-R²)=2Rr², h=2Rr²/(r²-R²).
Since R is a given constant, we have h in terms of r, so we can express the volume of the cone in terms of r:
V=⅓πr²(2Rr²/(r²-R²))=⅔πRr⁴/(r²-R²).
The rate of change of volume with respect to r is:
dV/dr=(⅔πR)(4r³(r²-R²)-2r⁵)/(r²-R²)².
dV/dr=(⅔πR)(2r⁵-4r³R²)/(r²-R²)².
When the volume is maximum or minimum, dV/dr=0, so 2r⁵-4r³R²=0, and 2r³(r²-2R²)=0. r=0 is the minimum, and r=R√2 is the maximum.
When r=R√2, h=2Rr²/(r²-R²)=4R³/R²=4R and the maximum volume of the cone is ⅓π(2R²)(4R)=(8/3)πR³.
So for max volume, r=R√2 and h=4R.