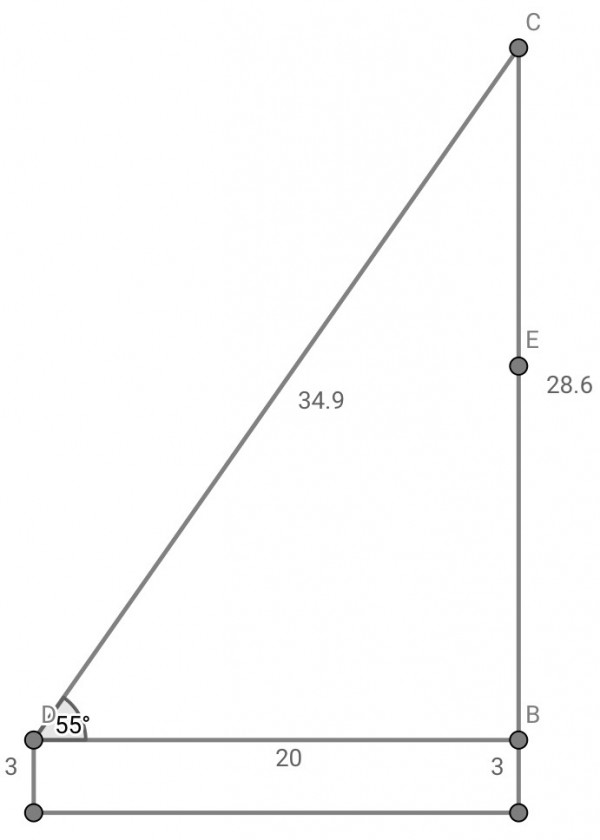
If D is the end of the rope at David’s end (round his waist) and C is where the rope reaches the carabiner, then DC=48-h where h is the vertical distance CE between Emily (E) and the carabiner.
cos(55)=20/(48-h)=DB/CD because David is 20 ft from the wall and the rope length in total is 48 ft. The legs of a right triangle CDB are 20 (base DB) and CB (wall), with hypotenuse CD and B is the point on the wall opposite D.
(1) Therefore CD=48-h=20/cos(55)=34.8689 ft=34.87ft approx.
(2) h=CE=48-34.8689=13.1311 ft. So Emily is 13.1311 ft from the carabiner. CB=20tan(55)=28.563 ft. So the height of the carabiner is 28.563+3=31.563ft above ground, and Emily’s climbed height is 31.563-13.1311=18.43ft approx.