Since point A is on the y-axis (x=0) then plug x=0 into the equation of the line x-2y+8=0 and we get y=4, so A is at (0,4). Since B is a right angle, BC is perpendicular to AB which means that the slope of the line of which BC is a segment has a slope of -2 because the AB line has a slope of ½ (y=½x+4). So the perpendicular has the equation y-2=-2(x-6), slope intercept form, plugging in C(6,2). This gives us y=-2x+14. Point B is where the two lines intersect: ½x+4=-2x+14, equating the y values. So 5x/2=10, x=10×⅖=4, and y=6 (½(4)+4 or -2(4)+14).
(i)
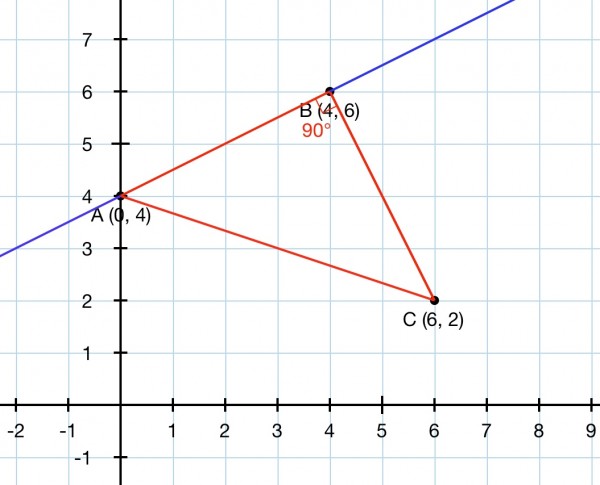
The triangle ABC is in red, and the line containing AB is blue.
(ii) BC is the equation 2x+y-14=0. Slope of AC is (2-4)/(6-0)=-⅓ and the equation is y-4=-⅓x, that is, x+3y-12=0.