Question

Let C be a circle with radius 1 centred at the point (2, 0). Write parametric equations to traverse C once, in a clockwise direction, starting from the point (2, −1).

Answer 1

For any angle t:

sin²(t)+cos²(t)=1.

The equation of C in rectangular coordinates is:

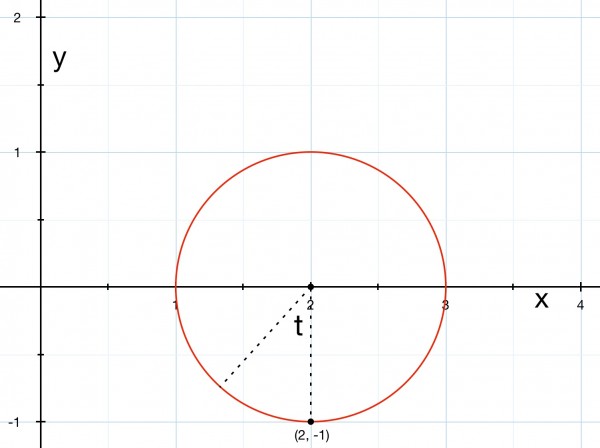
(x-2)²+y²=1.

Therefore we can equate coordinates to a parameter t.

If we define t as the angle the radius makes with the negative vertical y axis, then x=sin(t). So x-2=sin(t) and the parametrised equations are:

x=sin(t)+2, y=cos(t). The starting point for t=0 then corresponds to the point (2,-1).

The finishing point is t=2π for one complete cycle.

With this definition of t in mind we have:

x=sin(t)+2 and y=cos(t) for t ∈[0,2π].

This can be written (sin(t)+2,cos(t)) t ∈[0,2π].

 

For an exact match with the rectangular coordinates, we can introduce a phase shift and replace t with t+π, making sin(t)+2 into sin(t+π)+2=2-sin(t) and cos(t) into cos(t+π)=-cos(t).

The parameterisation becomes:

(2-sin(t),-cos(t)) for t ∈[0,2π].

t=0⇒(2,-1) and t=2π⇒(2,-1)—complete cycle;

t=π/2⇒(1,0), t=π⇒(2,1), t=3π/2⇒(3,0).