For any angle t:
sin²(t)+cos²(t)=1.
The equation of C in rectangular coordinates is:
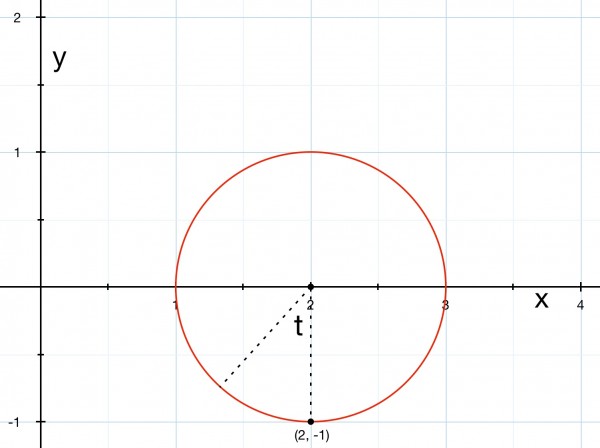
(x-2)²+y²=1.
Therefore we can equate coordinates to a parameter t.
If we define t as the angle the radius makes with the negative vertical y axis, then x=sin(t). So x-2=sin(t) and the parametrised equations are:
x=sin(t)+2, y=cos(t). The starting point for t=0 then corresponds to the point (2,-1).
The finishing point is t=2π for one complete cycle.
With this definition of t in mind we have:
x=sin(t)+2 and y=cos(t) for t ∈[0,2π].
This can be written (sin(t)+2,cos(t)) t ∈[0,2π].
For an exact match with the rectangular coordinates, we can introduce a phase shift and replace t with t+π, making sin(t)+2 into sin(t+π)+2=2-sin(t) and cos(t) into cos(t+π)=-cos(t).
The parameterisation becomes:
(2-sin(t),-cos(t)) for t ∈[0,2π].
t=0⇒(2,-1) and t=2π⇒(2,-1)—complete cycle;
t=π/2⇒(1,0), t=π⇒(2,1), t=3π/2⇒(3,0).