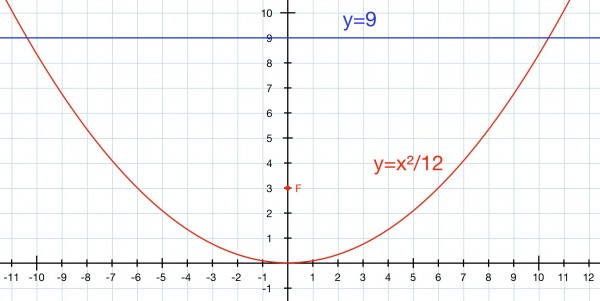
The paraboloid has two cross-sections: circle and parabola, illustrated below in 2D and 3D. In the 3D projection (which can be viewed using 3D glasses—left eye red filter, right eye—green/blue filter) a horizontal plane intersects the paraboloid 9in from the vertex. In the 2D vertical section, the parabola with its focus can be seen and the blue line intersects the parabola. The blue line is the plane in the 3D projection as seen on edge. The equation of the 2D picture is y=x²/4f=x²/12 where f is the focus at 3in when (0,0) is the vertex.
The radius of the searchlight can be calculated by putting y=9:
9=x²/12, x²=108=r² where r is the required radius. r=√108=6√3=10.39in. approx.

Equation of paraboloid: z=(x²+y²)/12.