Question

Apply each transformation or sequence of transformations of the function f (x) = 3x^2 : then determine how it/they affect the number of zeros the function has. 

1. a)  a vertical stretch of factor 2

2. b)  a horizontal translation 3 units to the left

3. c)  a horizontal compression of factor 2 and then a reflection 


   in the x-axis

4. d)  a vertical translation 3 units down

5. e)  a horizontal translation 4 units to the right and then a vertical translation 


   3 units up

6. f)  a reflection in the x-axis, then a horizontal translation 1 unit to the left, 


   and then a vertical translation 5 units up

Answer 1

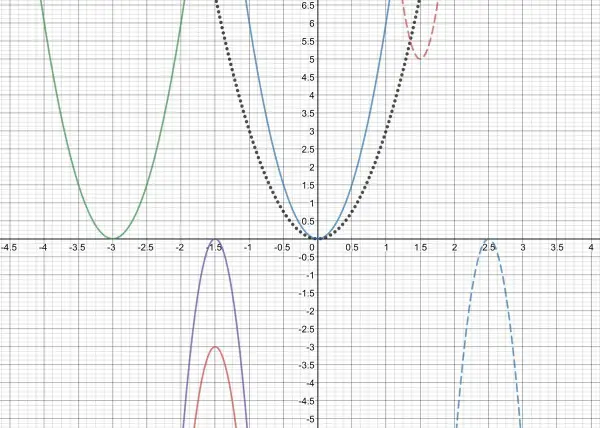
The transformations are shown in steps by colour-coded parabolas. The dotted black parabola is the original function.

a) blue: f(x)=6x² b) green: f(x)=6(x+3)² c) purple: f(x)=-6(2x+3)² d) red: f(x)=-6(2x+3)²-3 e) dashed blue: f(x)=-6(2(x-4)+3)²=-6(2x-5)² f) dashed red: f(x)=6(2(x+1)-5)²+5=6(2x-3)²+5.

One way to track the transformations is to follow the vertex which starts at the origin.

The original function had one zero at x=0. The transformations have a zero (non-complex) only when the vertex lies on the x axis.