Find distance of point from a line

Question

Find distance of point A on line BC where A(1,4,-2) B(2,1,-2) C(0,-5,1)

Answer 1

To find the vector BC, in the direction B to C, we can write the vector equation: OC-OB=BC, where O is the origin of the frame of reference.

So BC=(0,-5,1)-(2,1,-2)=(0-2,-5-1,1-(-2))=(-2,-6,3).

And AC=OC-OA=(0,-5,1)-(1,4,-2)=(-1,-9,3).

The dot product of AC and BC can be used to find the angle ACB:

AC.BC=|AC||BC|cosACB, where || means the magnitude, or length, of the vectors, which we find by using AC.AC=AC²,

so |AC|=√(AC.AC)=√(1+81+9)=√91 and similarly |BC|=√(4+36+9)=7.

Therefore (-1,-9,3).(-2,-6,3)=2+54+9=65=7cosACB√91.

If N is the point on BC such that AN is perpendicular to BC, then we have a right triangle ACN where N is the right angle and cosC=cosACB=65/(7√91). We don’t need to consider the sides of the triangle as vectors because we are only dealing with side lengths and angles between the sides, so AN is simply the side length.

But AN, the shortest distance between A and BC,=|AC|sinC.

sinC=√(1-cos²C)=√(1-325/343)=(3/7)√(2/7)=6/(7√14).

Therefore AN=(√91)(6/(7√14))=(6/7)√(91/14)=(6/7)√6.5=2.1853 linear units approx.

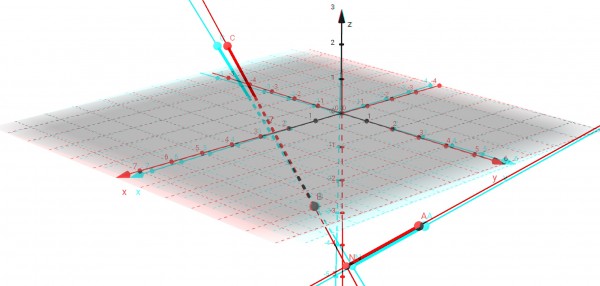
The picture is best viewed using a 3D viewer (right lens green/blue, left lens red). Acknowledgements to GeoGebra for their free app.