If r is the ratio, 1/(1-r)=70, 1-r=1/70, so r=69/70.
The reason is that the length of the ladder is the sum of the series 1+r+r²+r³+... where r<1 where 1 is the distance between the ground and first rung (12 inches=1 foot). The second rung is 69/70 ft (about 11.83 inches) from the first rung, and the third rung is (69/70)² ft = 0.9716 ft (approx 11.66 inches) from the second rung, and so on. There are an infinite number of rungs. The sum to infinity is 1/(1-r).
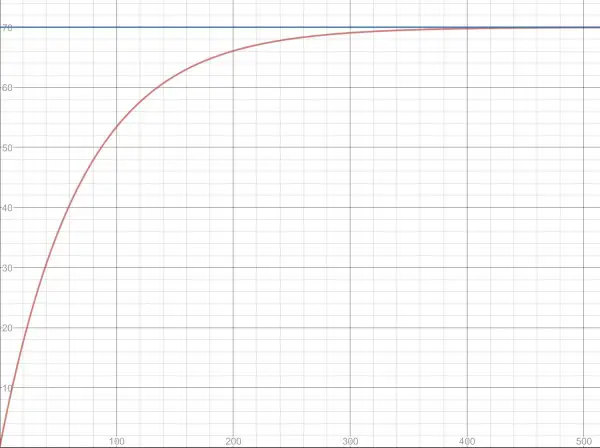
Note that the ratio is a fraction, not the number of inches. If the distance between the rungs was decreased by a fixed number of inches it would not be a ratio. The graph below shows a fixed ratio of 69/70. The x-axis shows how many rungs would make the length of the ladder the value on the y-axis. The blue line is an asymptote at 70 feet, and an infinite number of rungs is needed to get to that length. As x gets bigger the length of the ladder gets closer to 70 feet.
If a fixed decrement (not a ratio) of 12/139 of an inch is applied to each rung then there will be 139 or 140 rungs. 12/139" is the maximum fixed decrement.