x²/2+y²/2+z²-xy=4.
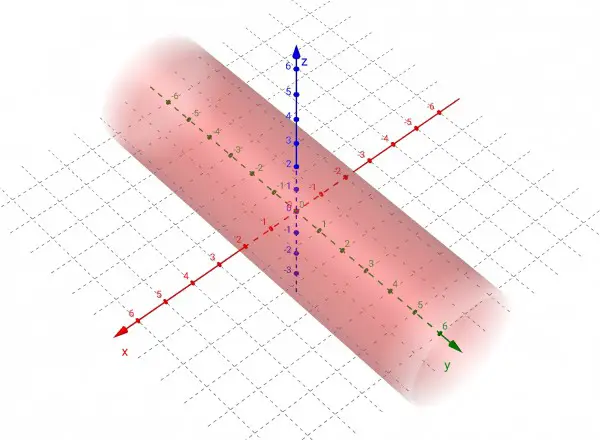
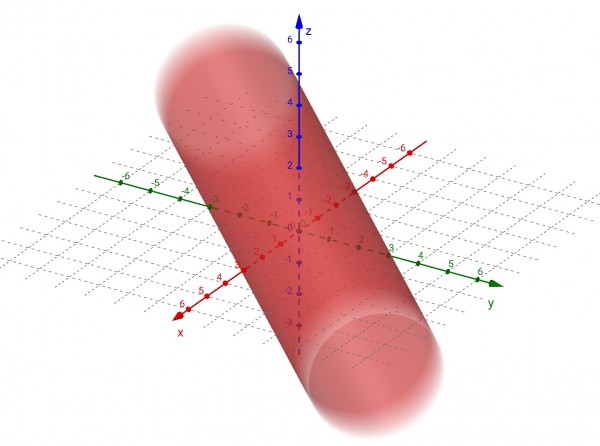
Tilting in the x-z plane has no effect because the y-axis is the axis of symmetry of the cylinder and the cross-section is a circle which remains a circle however rotated. Viewing the cylinder looking at the y-z plane (that is, looking along the x-axis) the cylinder is enclosed in the lines z=2 and z=-2. When the cylinder is swivelled clockwise through 45 degrees, its axis of symmetry which was the y-axis, becomes the line y=x (z=0).
Let O be the origin of the three axes. Take any point P(x,y,z) in the 3-space. Let r=OP, the distance between the origin and the point. If P is projected onto the x-y plane to point Q in this plane, PQ is the height of P above the plane, that is, z=PQ. Similarly, if P is projected onto the y-z plane to point R in this plane, x=PR. OR is at an angle ɸ to the y-axis, and OQ is at an angle θ to the y-axis.
The picture below is best viewed using 3D glasses (red filter for left eye, green or blue filter for right eye). θ is angle QON and ɸ is POQ.
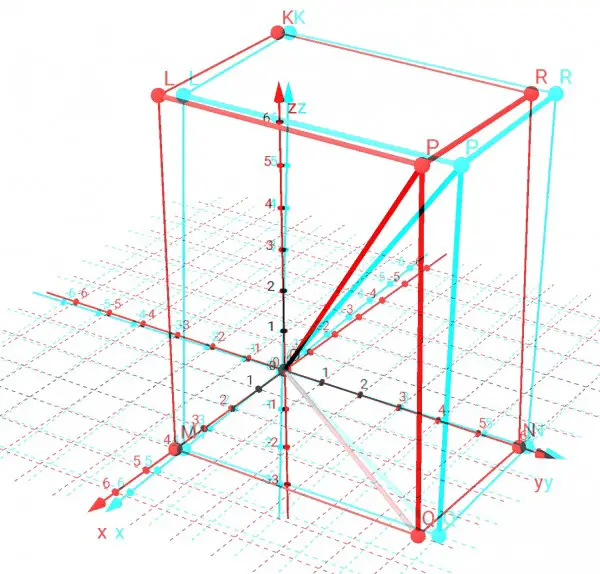
We can now write: z=rsinɸ, OQ=rcosɸ, from which y=OQcosθ=rcosɸcosθ and x=OQsinθ=rcosɸsinθ. You can see that r²=x²+y²+z². If P is rotated about the z-axis clockwise 45 degrees to a position P'(x',y',z') then angle θ is increased by 45 degrees, so we can work out the coordinates of P'. x'=rcosɸsin(θ+45)=rcosɸ(sinθ/√2+cosθ/√2) because sin45=cos45=1/√2. Also y'=rcosɸcos(θ+45)=rcosɸ(cosθ/√2-sinθ/√2). Using the values for x and y we had earlier we can replace the trig functions: x'=(x+y)/√2, y'=(y-x)/√2, z'=z because z is unaffected by the rotation about the z-axis. So x'+y'=2y/√2=y√2, and y=(x'+y')/√2; x'-y'=2x/√2=x√2, and x=(x'-y')/√2. To get the equation of the tilted cylinder we can substitute these values into the given equation: x²+z²=4⇒(x'-y')²/2+z'²=4, (x'²-2x'y'+y'²)/2+z'²=4. This gives us (x'²+y'²)/2+z'²-x'y'=4. The prime notation can now be dropped because this gives us the general relationship between the orthogonal coordinates, regardless of how the axes are labelled.
(Acknowledgements to GeoGebra Graphing Calculator for their wonderful free app!)