Gh There are two diagonals and the given points haven’t been labelled, so I need to give two answers.
The base and top have a length of 6-(-2)=8 units, 11-3=8 units.
The top is shifted 3-(-2)=5 units to the right of the base. If we drop a perpendicular on to the base it intercepts the base at (3,-4) forming a right triangle (3,2), (3,-4), (6,-4) where (3,-4) is the right angle. The hypotenuse is a diagonal so its length is √(3²+6²)=√45.
That’s one diagonal. Now for the other. Drop a perpendicular from the top right vertex (11,2) on to the extended base at (11,-4). The right triangle has a base length of 11-(-2)=13 units and a height of 2-(-4)=6 units just like the other diagonal. So, again using Pythagoras’ Theorem, the length of this second diagonal is √(13²+6²)=√205.
So the diagonals have lengths √45=6.7082 approx and √205=14.3178 approx units.
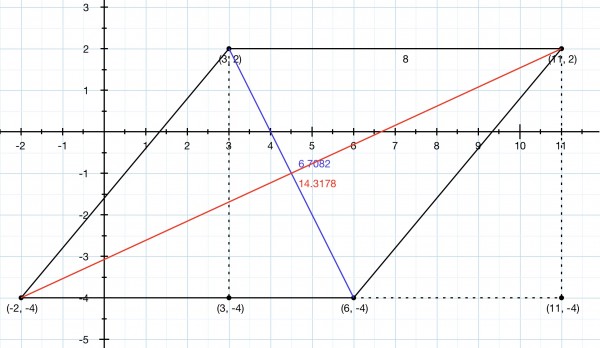
Check your question and label the vertices so that you can tell whether it’s the red or blue diagonal implied in the question.