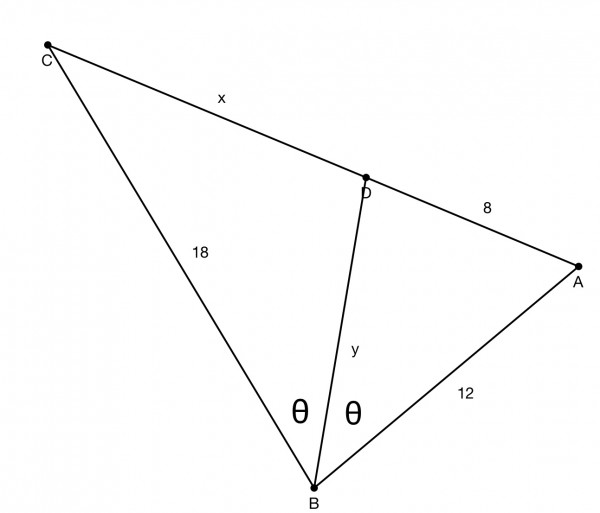
The angle bisector splits triangle ABC into two triangles ADB and DBC. The sum of the areas of the two triangles equals the area of ABC. We use the formula ½bcsinA where A is the angle between two sides. So we can write ½AB.BDsinθ+½BC.BDsinθ=½AB.BCsin(2θ) where 2θ is the measure of angle B. Let x=DC and y=BD and substitute AB=12 and BC=18:
6ysinθ+9ysinθ=108sin(2θ)=216sinθcosθ.
sinθ can be cancelled out: 15y=216cosθ and cosθ=15y/216=5y/72. Whenever we encounter cosθ in other equations we can replace it with 5y/72.
In triangle ABD we can apply the Cosine Rule.
8²=y²+12²-24ycosθ=y²+144-24y(5y/72).
So: 64=y²+144-5y²/3. ⅔y²=80, y²=120.
In triangle DBC we can apply the Cosine Rule.
x²=y²+18²-36ycosθ=y²+324-36y(5y/72).
So: x²=y²+324-5y²/2=324-3y²/2=324-360/2=144, and x=12.
x=DC=12.