Using the Taylor expansion for two variables x and y up to the second degree at the point (a,b) we have:
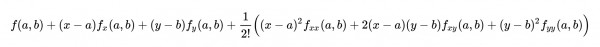
Let f(x,y)=x²cos(x+y) and (a,b)=(0.1,e).
fᵪ=∂f/∂x=2xcos(x+y)-x²sin(x+y); fᵧ=∂f/∂y=-x²sin(x+y)
fᵪᵪ=2cos(x+y)-4xsin(x+y)-x²cos(x+y); fᵧᵧ=-x²cos(x+y)
fᵪᵧ=fᵧᵪ=-2xsin(x+y)-x²cos(x+y)
T2(x,y)=0.01cos(0.1+e) + (x-0.1)(0.2cos(0.1+e) - 0.01sin(0.1+e)) - 0.01(y-e)sin(0.1+e) + ½((x-0.1)²(2cos(0.1+e) - 0.4sin(0.1+e) - 0.01cos(0.1+e)) - 2(x-0.1)(y-e)(0.2sin(0.1+e) + 0.01cos(0.1+e)) - 0.01(y-e)²cos(0.1+e)).