The graph looks complicated but it contains enough information to answer the question.
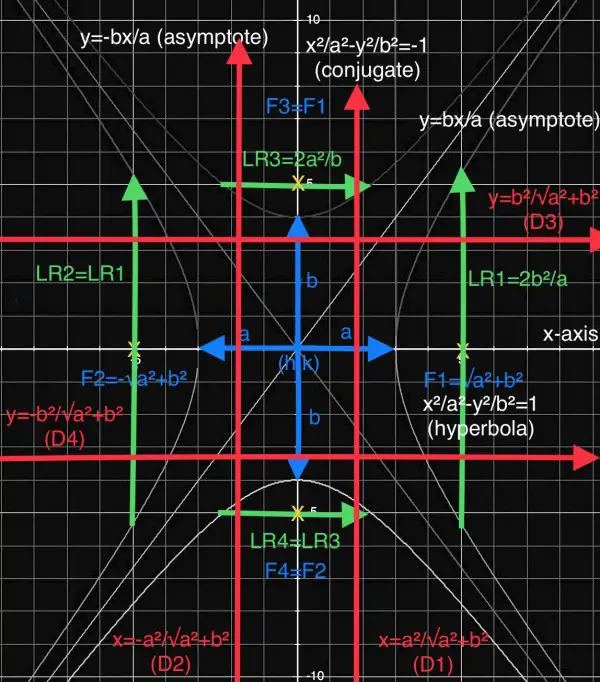
The origin of the graph is marked (h,k) representing a displacement from (0,0). All the text is based on hyperbolas that have their origin at (0,0) to keep the formulas as simple as possible.
Colour-coding aids legibility: the green arrows and text show the latus recta (LR1 to LR4); the red arrows and text show the directrices (D1 to D4); blue shows foci, a and b in the hyperbola formulae; shades of grey show the hyperbolas, axes, asymptotes and grid lines. The yellow crosses mark the foci F1 to F4.
The left-right orientated hyperbola is the “normal” hyperbola with its transverse (major) axis as the x-axis. The associated conjugate hyperbola is up-down and the conjugate (minor) axis is the y-axis. Both hyperbolas have the same asymptotes shown as y=bx/a and y=-bx/a. The centre is at (h,k)=(2,-5). One hyperbola is the conjugate of the other. F1, F2, LR1, LR2, D1, D2 apply to the hyperbola (normal left-right), while the remaining labels apply to the conjugate hyperbola.
The distance between the foci is 2√a²+b² as can be seen by the yellow crosses. So √a²+b²=√145 and a²+b²=145. The numerical value of the asymptote slope is b/a. “Conjugate parallel to the y-axis” I understand to mean the conjugate axis is parallel to the y-axis, so the transverse axis of the hyperbola is parallel to the x-axis. The equation of the conjugate axis is x=h=2, and that of the transverse axis is y=k=-5. This means we need the equation of the left-right hyperbola for which LR=2b²/a. So b/a=2b²/16a=b²/8a, and b=8. a²+b²=145, a²=145-64=81.
We need to adjust the origin, or centre, of the hyperbola so in place of x we need x-5 and in place of y, y+5.
The equation of the hyperbola is (x-2)²/81-(y+5)²/64=1.