Considering two linear segments and part of a parabola, find the equations of the three segments.

Question

L1: y=mx+k  [slope = 0.8]  x<=0  P(0,0)

L2: y=mx+k  [slope = -3.3]  x>=16

f(x)=ax^2 +bx+c  0<=x<=16  Q(16,y)

* The straight lines link to the parabola at points P and Q respectively

* To ensure smooth connections between the linear segments and the parabola, L1 and L2 need to be tangents to the parabola f(x) at the connection points P and Q. P is at the origin and the horizontal distance from P and Q is 16 units.

Answer 1

f(x)=ax²+bx+c, f'(x)=2ax+b.

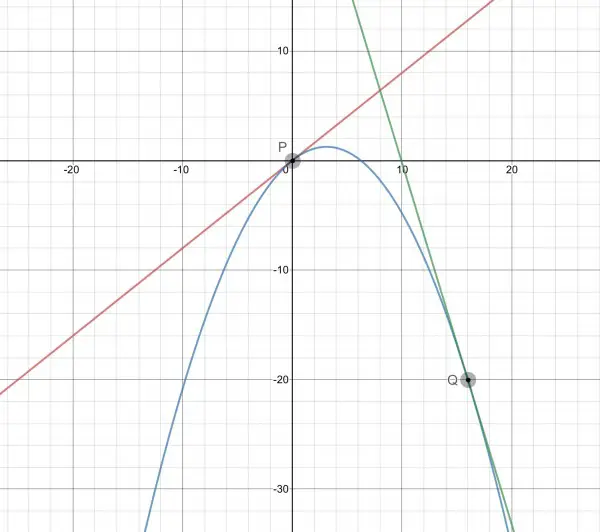
At P(0,0), f'(0)=b and at Q(16,y), f'(16)=32a+b.

L1 is tangential at P, and its gradient has to be that of the parabola, so b=0.8 and f'(16)=32a+0.8.

For L1, y=0.8x+k. The point P(0,0) lies on L1 and f(x), therefore: 

k=c=0,

f(x)=ax²+0.8x, 

y=0.8x is L1.

At Q(16,f(16)), f'(16)=32a+0.8=-3.3 because L2 has the same gradient as f(x) at Q, so 32a=-4.1, a=-4.1/32. y=f(16)=256a+12.8=-32.8+12.8=-20. Therefore Q is at (16,-20).

f(x)=-4.1x²/32+0.8x.

For L2, y=-3.3x+k, so plug in x=16, y=-20:

-20=-52.8+k, k=32.8 and L2 is y=-3.3x+32.8.

The graph shows two lines and a parabola where L1 is red, L2 is green  and f(x) is blue. These are shown without segmentation.

L1 ceases at P where it joins f(x). The next segment tracks f(x) up to Q, where it joins the start of L2, and segment L2 continues downwards.