cos(3x-50)=sin(90-(3x-50))=sin(140-3x); so 5x-28=140-3x; 8x=168, x=21°.
Also: sin(5x-28)=sin(180-(5x-28))=sin(208-5x); so 208-5x=140-3x; 2x=68, x=34°.
CHECK
3x-50=63-50=13; 5x-28=105-28=77; sin77=cos13 because 77+13=90.
3x-50=102-50=52; 5x-28=170-28=142; sin142=cos52=sin38 because 180-38=142.
Three solutions: x=21°, 34° and 66°, because sin(5x-28)=sin302 and cos(3x-50)=cos148=sin(90+58).
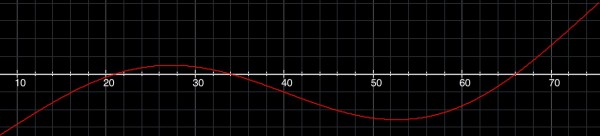
The graph of sin(5x-28)-cos(3x-50) crosses the x-axis at three points between x=0 and x=90: x=21, 34, 66. These are the three solutions for x. We can therefore be sure we have found all the solutions.