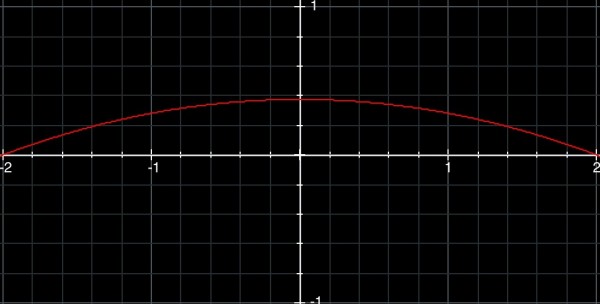
The area under the curve = 1 the sum total of all probabilities.
For continuous random variable, summation is replaced by integration.
(a) P(x>0)=0.09375∫(4-x^2)dx{0,2}=0.09375[4x-x^3/3]{0,2}=0.09375(8-8/3)=0.5 (confirmed by picture)
(b) P(-1<x<1)=0.09375[4x-x^3/3]{-1,1}=0.09375(4-1/3-(-4+1/3)=0.09375(8-2/3)=0.6875. Note that because of symmetry this is the same as 2*0.09375[4x-x^3/3]{0,1}.
(c) 1, because this covers the whole of x between -2 and 2. The area to the left of x=0.5 and the area to the right include all x. So x has to be in one or other of the areas.
(d) P(0<x<1.5)=0.09375[4x-x^3/3]{0,1.5}=0.09375(6-1.125)=0.45703125.
Therefore P(x>1.5)=0.5-0.45703125=0.04296875, because 0.5 of the area is on the right (>0) so we merely subtract P(0<x<1.5). The picture makes this clearer.