Find the equation of a straight line

Question

Show on a diagram the position of the straight line xcos30°+ysin30°=2 in relation to the co-ordinate axes, indicating clearly which angle is 30° and which length is 2 units. Find:-

i)the equatiion of the straight line parallel to that given line and passing through the point (4,3);

ii)the length of the perpendicular from the origin on to this line;

iii)the distance between the two parallel straight lines.

Answer 1

ysin30=-xcos30+2; y=-xtan60+2cosec30=-xtan60+4=-x√3+4. When x=0, y=4 (y-intercept), y=0, x=4√3/3.

(i) The slope of the line is -tan60=-√3 and this is also the slope of the parallel line which has the equation:

y-3=-tan60(x-4) in slope-intercept form.

Therefore y=3-xtan60+4tan60=3+4√3-x√3 or xcos30+ysin30=3sin30+4cos30.

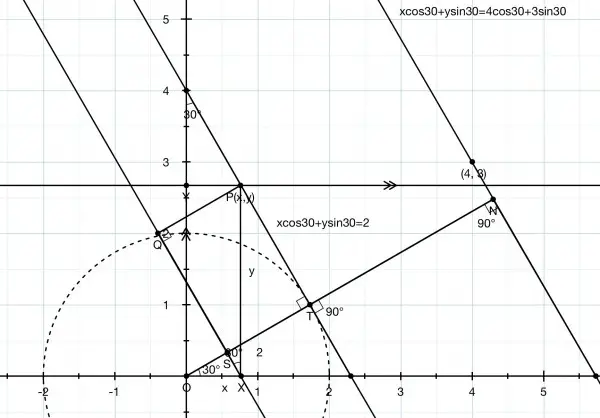
For a general point P(x,y) on the line, OX=YP=x and OY=XP=y. OT=OS+ST=OS+QP.

OS=xcos30 and QP=ysin30, so OT=xcos30+ysin30=2. OT is the radius of the circle of which the line xcos30+ysin30=2 is a tangent.

(ii) ON is the length of the perpendicular on to the parallel line xcos30+ysin30=4cos30+3sin30. By analogy, ON=4cos30+3sin30=2√3+3/2 just as OT=2 for the other line.

(iii) The distance between the lines must therefore be the difference in the two radii, ON-OT=2√3+3/2-2=2√3-1/2.