Quadrilateral WXYZ has right angles at angle W and angle Y and an acute angle at angle X. Altitudes are dropped from X and Z to diagonal WY, meeting WY at O and P. Prove that OW = PY.

Question

http://www.mathhomeworkanswers.org/?qa=blob&qa_blobid=16319575071232513539

Answer 1

http://brainly.com

Answer 2

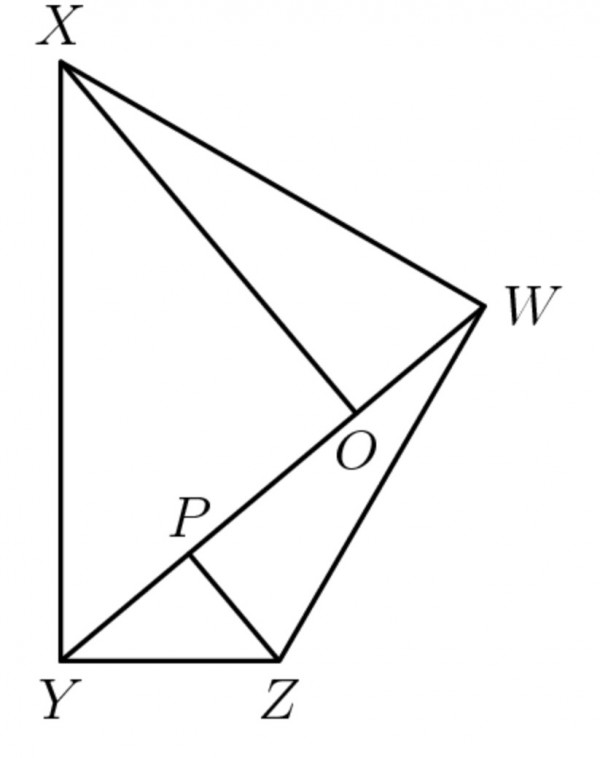
Consider the diagonal WY split into segments: PY, OP and OW.

Let x=PY, y=OP, z=OW.

The following right-angled triangles are similar: OWX, PWZ; OXY, PYZ, because we have complementary angles in right-angles triangles and we have complementary angles as a result of split right angles.

We can write the following side ratios: OW/OX=PZ/PW; OX/OY=PY/PZ. OW=OX.PZ/PW, and PY=OX.PZ/OY, so OW/PY=OY/PW, which means that if OW=PY then OY=PW. OY=x+y; PW=y+z. So z/x=(x+y)/(y+z). Cross-multiply: z(y+z)=x(x+y); yz+z^2-x^2-xy=yz+(z-x)(z+x)-xy=y(z-x)+(z+x)(z-x)=(x+y+z)(z-x)=0. Therefore x+y+z=0, which isn't true so z-x=0 and z=x, i.e., OW=PY (and OY=PW).

Incidentally, the other diagonal XZ can be considered as the diameter of a circle that circumscribes the quadrilateral. The right angles at W and Y are simply created by the semicircles for each half of the quadrilateral.