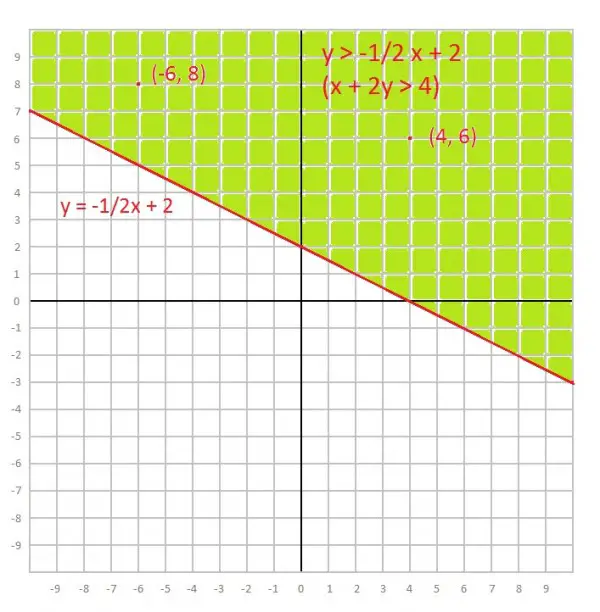
Problem: Which of the following is a graph of the inequality x + 2y > 4?
The point (4, 6) does not satisfy the inequality. Shade the side of the line that does not contain (4, 6). This is the solution.
You are WRONG! The point (4, 6) definitely DOES satisfy the inequality.
x + 2y > 4
4 + 2(6) > 4
4 + 12 > 4
16 > 4
Maybe you are trying to use new math, or, even worse, Common Core math, but
for centuries, 16 has ALWAYS been greater than 4.
Start by re-writing the inequality as an equality and plot the line it
represents.
x + 2y > 4
x + 2y = 4
x + 2y - x = -x + 4
2y = -x + 4
2y/2 = (-x + 4)/2
y = (-x + 4)/2
y = -1/2 x + 2
Because the inequality states "greater than," you can pick any point above
the plotted line, use the x and y co-ordinates of that point in the inequality,
and it will be true.
We have already shown that (4, 6) satisfies the inequality.
How about (-6, 8). It is above the line on the graph. Does it satisfy
the inequality?
x + 2y > 4
-6 + 2(8) > 4
-6 + 16 > 4
10 > 4
Yes, 10 is greater than 4.
Did you, perhaps, mean LESS THAN?