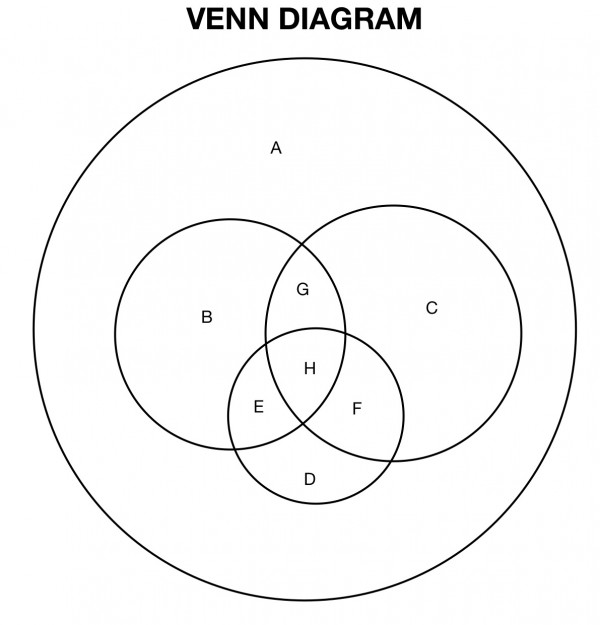
The problem can be solved using the above diagram. The three interlocking circles represent the subject teachers (maths, physics, chemistry). The letters are regions created by the circles. The solution consists of relating the lettered regions to facts given in the problem.
The large circle is all teachers. The regions are as follows (some regions may be zero):
A Teachers of other subjects
B Only maths
C Only physics
D Only chemistry
E Maths & chemistry but not physics
F Physics & chemistry but not maths
G Maths & physics but not chemistry
H All 3 subjects
Now we use the numbers in the problem:
A+B+C+D+E+F+G+H=60 (all teachers)
C+F+G+H=27 (physics)
B+E+G+H=30 (maths)
D+E+F+H=21 (chemistry)
G+H=12 (maths & physics & maybe chemistry)
E=0 (no-one teaches maths and chemistry)
H=0 because E=0, so no-one can teach all 3 subjects
So G=12, C+F=15, D+F=21, B=18
A+18+15+D+12=60, A+D=15. Assume A=0 (no teachers of other subjects) then D=15 and F=6 (physics and chemistry) and C=9 (only physics).