z^4+81=(z^2-9i)(z^2+9i).
But we need to take this further.
We need to find √i. Let a+ib (a and b are real) be equal to √i, then a^2+2aib-b^2=i. Matching real and imaginary parts, a^2=b^2 and 2ab=1. So a=b appears to be a solution and 2a^2=2b^2=1, making a=b=√2/2 (another way of writing 1/√2).
a=-b is another solution but this would give 2a^2=-1 which would make a imaginary. Therefore √i=(1+i)√2/2.
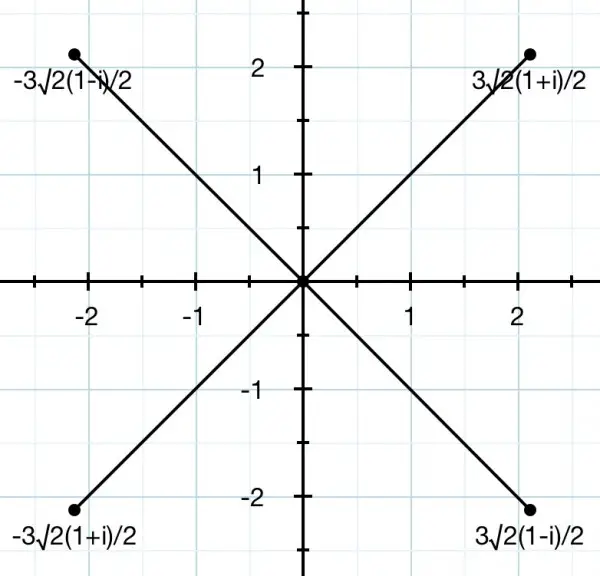
z^2-9i=(z-3√i)(z+3√i)=(z-3√2(1+i)/2)(z+3√2(1+i)/2). So two roots are ±3√2(1+i)/2.
z^2+9i=(z+3i√i)(z-3i√i) which gives us the roots ±3i√2(1+i)/2.
This becomes ±3√2(1-i)/2. So we now have the four roots.
These roots are represented by the lines in the above Argand diagram.