How do you prove this: a ^3cos(B-C) + b^3cos(C-A) + c^3cos(A-B) = 3abc

Question

a ^3cos(B-C) + b^3cos(C-A) + c^3cos(A-B) = 3abc

Answer 1

X = a³cos(B-C) + b³cos(C-A) +c³cos(A-B)

From sine rule and 3A trig identity a³ = 8R³sin³(A) = 2R³(3sin(A)−sin(3A))

So X = 2R³ ∑( 3sin(A)−sin(3A) )cos(B−C) = R³Y where ∑ is over cycles

2sin(A)cos(B−C) = sin(A+B−C) + sin(A−B+C) = sin(2C) + sin(2B)

2sin(3A)cos(B−C) = sin(3A+B−C) + sin(3A−B+C)

with similar expressions for B,C,A & C,A,B

∴ Y = 3∑sin(2C) + 3∑sin(2B) − ∑sin(3A+B−C) − ∑sin(3A−B+C)

∑sin(3A+B−C) + ∑sin(3A−B+C) = sin(3A+B−C) + sin(3B+C−A) + sin(3C+A−B) +
                                                  sin(3A−B+C) + sin(3B−C+A) + sin(3C−A+B) … (i)

But (3A+B−C) + (3C−A+B) = 2(A+B+C) = 2π so sin(3A+B−C) + sin(3C−A+B) = 0 with similar for other pairs of terms in (i). So (i) is zero.

∴ Y = 6∑sin(2A) = 24sin(A)sin(B)sin(C) (an easily proved identity for a triangle)

Y = 24abc/(8R³) = 3abc/R³ → X = 3abc

Trigonometric Functions
 

Answer 2

https://answers.yahoo.com/question/index?qid=20130108012204AAQJZ7R provides one very good solution, even though it lacks some explanation of its terminology.

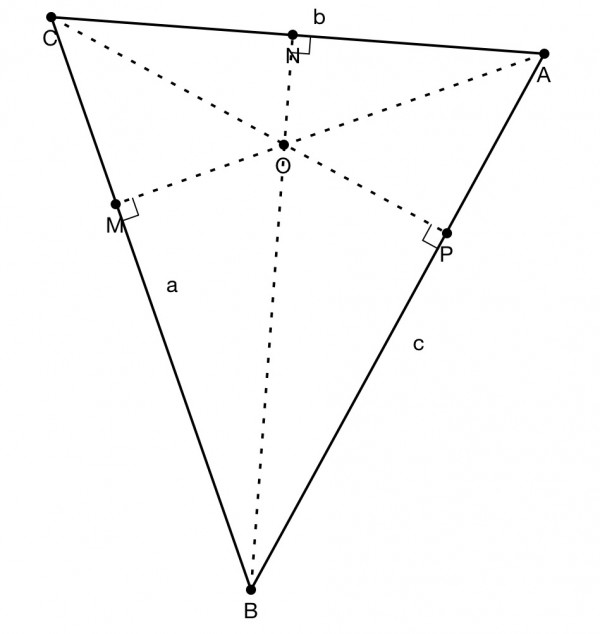
The picture shows a scalene triangle with perpendiculars from each vertex.

Because A+B+C=180,

cosA=-cos(B+C), cosB=-cos(C+A), cosC=-cos(A+B).

AM=bsinC=csinB; AN=ccosA=b-acosC; AP=bcosA=c-acosB;

BM=ccosB=a-bcosC; BN=csinA=asinC; BP=acosB=c-bcosA;

CM=bcosC=a-ccosB; CN=acosC=b-ccosA; CP=asinB=bsinA.

The sides a, b and c are also related thus:

a=bcosC+ccosB; b=acosC+ccosA; c=acosB+bcosA,

from which abc=(bcosC+ccosB)(acosC+ccosA)(acosB+bcosA).

Consider the expression (U+V)(W+X)(Y+Z)=(U+V)(WY+WZ+XY+XZ)=

UWY+UWZ+UXY+UXZ+VWY+VWZ+VXY+VXZ.

Substitute: U=bcosC, V=ccosB, W=acosC, X=ccosA, Y=acosB, Z=bcosA. UXY and VWZ combine to form the abc term:

a²bcosBcos²C+ab²cosAcos²C+

2abccosAcosBcosC+

b²ccos²AcosC+a²ccos²BcosC+ac²cosAcos²B+bc²cos²AcosB.

The difference of the angles can also be expanded:

cos(A-B)=cosAcosB+sinAsinB; cos(B-C)=cosBcosC+sinBsinC; cos(C-A)=cosCcosA+sinCsinA.

As can the sums:

cos(A+B)=cosAcosB-sinAsinB; cos(B+C)=cosBcosC-sinBsinC; cos(C+A)=cosCcosA-sinCsinA.

Note also that cos(A-B)+cos(A+B)=2cosAcosB; cos(B-C)+cos(B+C)=2cosBcosC; cos(C-A)+cos(C+A)=2cosCcosA; sin(A-B)+sin(A+B)=2sinAcosB; sin(B-C)+sin(B+C)=2sinBcosC; sin(C-A)+sin(C+A)=2sinCcosA.

And cosine of an angle sum can be replaced by those of a single angle, e.g., cos(A-B)+cos(A+B)=cos(A-B)-cosC=2cosAcosB.

abc=a²cosBcosC(bcosC+ccosB)+

b²cosCcosA(acosC+ccosA)+

c²cosAcosB(acosB+bcosA)+

2abccosAcosBcosC.

Because bcosC+ccosB=a, etc., this further reduces to:

abc=a³cosBcosC+b³​cosCcosA+c³​cosAcosB+2abccosAcosBcosC=
½(a³​(cos(B-C)+cos(B+C))+b³​(cos(C-A)+cos(C+A))+c³​(cos(A-B)+cos(A+B)))+2abccosAcosBcosC.

If we multiply both sides by 2 we get:

2abc=a³​(cos(B-C)+cos(B+C))+b³​(cos(C-A)+cos(C+A))+c³​(cos(A-B)+cos(A+B))+4abccosAcosBcosC.

cos(B+C)=-cosA, cos(C+A)=-cosB, cos(A+B)=-cosC.

2abc=a³​(cos(B-C)-cosA)+b³​(cos(C-A)-cosB)+c³​(cos(A-B)-cosC)+4abccosAcosBcosC.

This can be rearranged thus:

2abc=a³​cos(B-C)+b³​cos(C-A)+c³​cos(A-B)+4abccosAcosBcosC-a³​cosA-b³​cosB-c³​cosC.

Now, let's go back to the picture and consider one of the right-angled triangles. Let's pick ABM. In this triangle M is the right angle so cosM=0; the "new" a, b and c are respectively MB, AM and BC (as before).

So as to avoid confusion, the letters a', b', c', A', B', C' (the "new") will be used when these are used with respect to triangle ABM. The unprimed letters will be used in reference to the triangle ABC. Triangle ABM must also satisfy the general trig identity, so we can apply our logic to ABM just as it was applied to triangle ABC.

a'=MB=ccosB=a-bcosC, b'=AM=csinB, c'=c; A'=90-B'=90-B, B'=B, C'=90, sinA'=cosB'=cosB; cosA'=sinB'=sinB. 

4a'b'c'cosA'cosB'cosC'-a'³​cosA'-b'³​cosB'-c'³​cosC'=-a'³​cosA'-b'³​cosB', because cosC'=0,=

-a'³​b'/c'-b'³​a'/c'=-a'b'(a'²+b'²)/c'=-a'b'c', because a'²+b'²=c'², by Pythagoras.

By substituting backwards (reverse engineering) for a', b' and c' we can see how this reduction applies to the triangle ABC. We could have chosen any of the right-angled triangles within ABC and arrived at the same result.

So we have now the general case:

2abc=a³cos(B-C)+b³cos(C-A)+c³cos(A-B)-abc which means that

3abc=a³cos(B-C)+b³cos(C-A)+c³cos(A-B) QED.