teel me the equation of ellipse?

Question

the point m a lunar orbit nearest the surface of the moon is called perilune and the point farthest from the surface is called a polune. the "a pollo II" spacecraft with perilune altitude 110 km and a polune altitude 314 km (above the moon) find the equation of this ellipse if the radius of the moon is 1728 km and the center of the moon is at one focus.

Answer 1

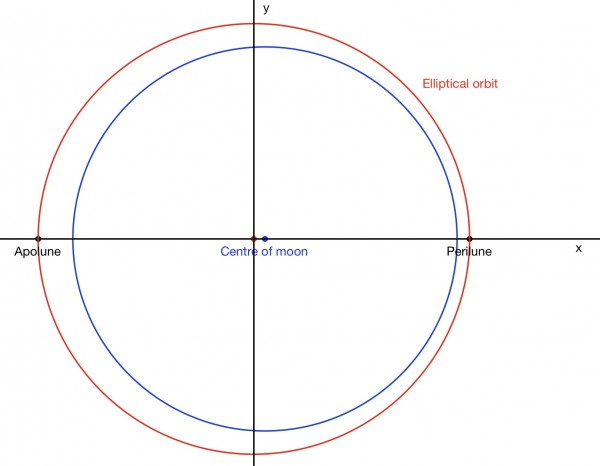
The radius of the moon is 1728km, so the perilune is 1728+110=1838km from one focus and the apolune is 1728+314=2042km  from the same focus. The general equation of an ellipse is x²/a²+y²/b²=1.

Therefore, when y=0, x=±a. The length of the major axis (the distance between perilune and apolune) is 2a=1838+2042=3880km, making a=3880/2=1940km. f²=a²-b² where f is the focus, so b²=a²-f². But f is the distance of the focus from the centre of the ellipse. We know a, the semi-major axis so f=1940-1838=102km and b²=1940²-102²=3753196..

The equation is x²/3763600+y²/3753196=1. The centre of the ellipse is at (0,0), as shown by the red point.