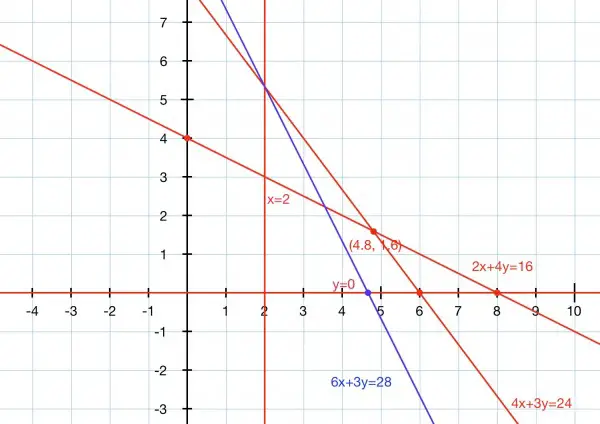
The graph shows the constraints as red lines. The inequalities are represented by areas, and the areas are defined by the constraints. The open area ABOVE both red sloping lines, to the right of x=2 and above the x-axis is the region where the inequalities are true, including the point where they intersect and all points on the lines themselves.
(The lines intersect where the system 2x+4y=16 (that is, x+2y=8) and 4x+3y=24 is solved. So we can write 4(8-2y)+3y=24, 32-8y+3y=24, 5y=8, y=1.6 and x=8-2y=8-3.2=4.8. The intersection point (4.8,1.6) is shown.)
The blue line is of the form 6x+3y=a, a constant. The minimum point for 6x+3y is when a has the smallest value, and that’s where the blue line is as far over to the left as possible so as to lie within the constraints. This is where x=2 on 4x+3y=24, so 3y=24-8=16, and y=16/3. Therefore a=12+16=28, and the blue line has the equation 6x+3y=28. The minimum value of 6x+3y=28.