It’s assumed that x and y are positive quantities including zero.
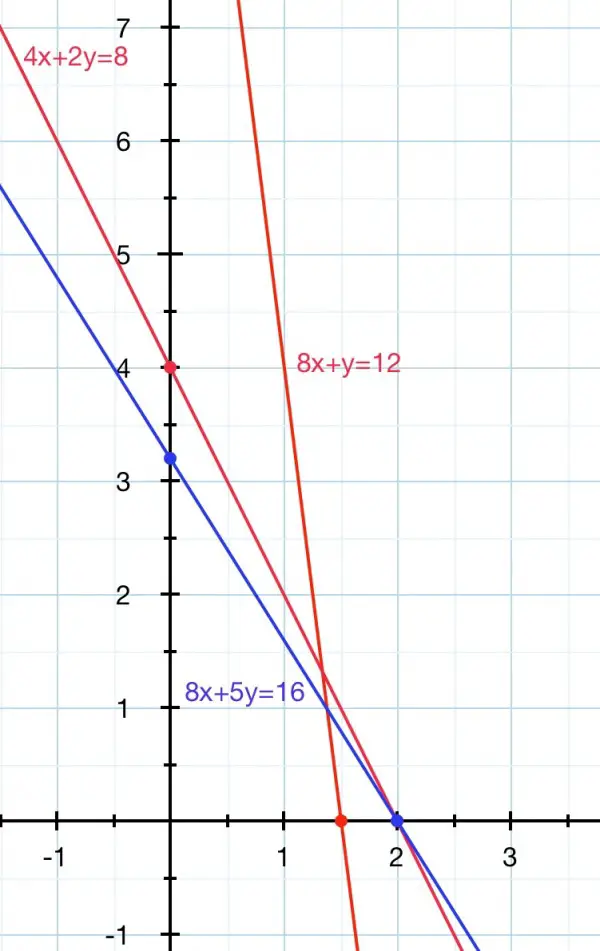
The red lines show the constraints. These lines are the given inequalities converted to equations. The open region bound by the axes and above both lines represent the inequalities. The axes are also constraints, ensuring that x and y are both greater than or equal to zero. The blue line z=8x+5y where z is a constant, has to be positioned as far left as possible so as to be in the defined region. The leftmost position for the blue line is where it meets 4x+2y=8 on the x axis (2,0). So z=8×2+0=16 and the blue line has the equation 8x+5y=16, the minimum value for z.
The intersection point is (4/3,4/3). If the blue line was shifted to pass through it, z would be 52/3 which is greater than 16, so the blue line would be further over to the right and z would not be minimum.