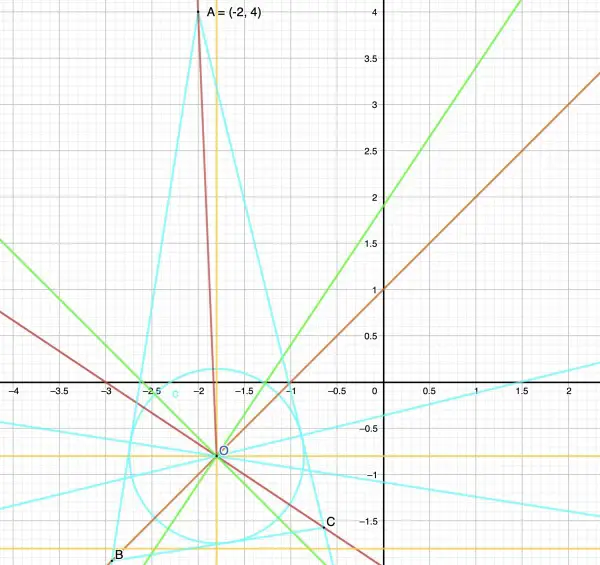
The question has been wrongly stated because, as the solution below will show, A(2,4) is outside the range of valid vertex coordinates. I suggest that A is the point (-2,4).
The bisector lines x-y+1=0 and 2x+3y+6=0 are shown in red along with the bisector of vertex A. The lines meet when y=x+1 meets y=-⅓(2x+6)=-⅔x-2 at O.
-⅔x-2=x+1, 5x/3=-3, x=-9/5=-1.8, so y=x+1=-0.8. O is at (-1.8,-0.8) as shown by the intersection of the orange lines at O.
The gradient of OA=(4-(-0.8))/(-2-(-1.8))=4.8/(-0.2)=-24. Let tanω=-24, the angle of the gradient.
The gradient of OB=1 (the coefficient of x in y=x+1), so the angle of the gradient is 45°.
The gradient of OC=-⅔. As an internal angle of triangle ABC, let tanη=⅔.
The three bisectors create three angles: between AO and BO, BO and CO, and AO and CO. From these angles we can calculate the vertex angles of ΔABC.
AÔB=180-ω+45=225-ω; BÔC=180-(45+η)=135-η; AÔC=ω+η. The sum of these is 360°, as expected.
Because of the bisectors we can write three equations involving half-angles:
(1) ½A+½B+225-ω=180,
(2) ½B+½C+135-η=180,
(3) ½A+½C+ω+η=180.
If we add these equations together we get A+B+C+360=540, A+B+C=180°, which confirms that we have vertex angles of ΔABC.
Equation (4)=(1)-(2)=½A-½C+90-ω+η=0; (4)+(3)=A+90-ω+η+ω+η=180, A=90-2η=2(45-η).
Therefore B=2(180-½A-225+ω)=2(180-45+η-225+ω)=2(η+ω-90) and C=2(180-½A-ω-η)=2(180-45+η-ω-η)=2(135-ω).
The picture shows the half-angles at vertex A radiating down towards the bisectors of B and C. AB and AC are shown as tangents to the pale blue incircle (labelled c). BC is also a tangent to the incircle and the radius of the incircle, centre O and perpendicular to AB and AC (pale blue) can be calculated.
All the angles as calculated above must be positive, otherwise ΔABC cannot exist. This places constraints on ω.
Angle A=2(45-η), and since η=arctan(⅔), and ⅔<1, where 1=arctan (45°), A>0, enabling us to draw the sides AB and AC, because of the intersection with the angle bisectors of B and C.
B=2(η+ω-90), so for B>0, η+ω>90, ω>90-η (about 56.31°). C=2(135-ω), so ω<135°. Therefore 90°-η<ω<135°. The green lines radiating upwards from O enclose the valid region for ω. It can be seen that (2,4) is outside this region, hence the given point A(2,4) prohibits a solution of the problem, whereas A(-2,4) lies within the region.
tan(½A)=tan(45-η)=(1-⅔)/(1+⅔)=⅕=0.2, so the length of the tangents from A=5r (r=radius of incircle) on AB and AC. Next we need to find the coordinates of B and C, knowing the length of OA. The gradient angle of AB is ω-½A=ω-45+η, and the gradient of AC is ω+½A=ω+45-η. The respective gradients are tan(ω-45+η)=tan(ω-(45-η))=(tanω-tan(45-η)/(1+tanωtan(45-η))=(-24-0.2)/(1-4.8)=-24.2/(-3.8)=121/19; and tan(ω+(45-η))=(tanω+tan(45-η)/(1-tanωtan(45-η))=(-24+0.2)/(1+4.8)=-23.8/5.8=-119/29. AB and AC pass through A(-2,4) so their line equations are:
y=(121/19)(x+2)+4 for AB and y=-(119/29)(x+2)+4 for AC. -119x-238+116=0, -119x=122
y=x+1=(121/19)(x+2)+4 at B, x=(121/19)(x+2)+3, 19x=121x+299, x=-299/102 and y=-197/102, hence B(-299/102,-197/102).
y=-⅔x-2=-(119/29)(x+2)+4 at C, -⅔x=-(119/29)(x+2)+6, -58x=-357x-714+522, x=-192/299 and y=-470/299, hence C(-192/299,-470/299). The horizontal gradient angle of BC has the same measure as the vertical angle of AB, so the tangent of this angle = cotangent of the vertical angle, making the gradient of BC=19/121 (see the picture for the geometry). This can also be deduced from the gradient between points B and C.
The equation of BC is y=(19/121)(x+299/102)-197/102 in slope-intercept form.