what is the integral of dt/t(1+absolute value of ln(t))^2

Question

what is the integral of dt/t(1+​|ln(t)|)^2

Answer 1

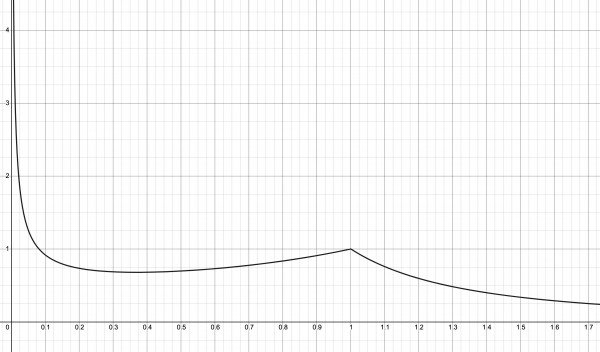
We can consider two integrals:

∫₀¹dt/(t(1-ln(t))²+∫₁^∞dt/(t(1+ln(t))²=∫dt/(t(1+|ln(t)|)², and let J be the first integral and the second K.

because between t=0 and t=1, ln(t) is negative so |ln(t)|=-ln(t)=ln(1/t); and in the interval [1,∞) |ln(t)|=ln(t).

Let x=1-ln(t), then -dx=dt/t; when t=1, x=1 and when t=0, x→∞, so the limits for J are x∈(-∞,1].

J=-∫_∞¹dx/x²=[1/x]_∞¹=1. Or we could revert to t: J=[1/(1-ln(t))]₀¹=1.

Let x=1+ln(t), then dx=dt/t; when t=1, x=1 and when t→∞, x→∞, so the limits for K are the same as for t.

K=∫₁^∞dx/x²=[-1/x]₁^∞. Reverting to t: K=[-1/(1+ln(t))]₁^∞=1.

So J+K=2. It would appear that the integral has become a definite integral, even though no limits were specified for the original integral.

However, see the graph below. The integral is the total area beneath the curve, which approaches asymptotically the y-axis on the left and the x-axis on the right, enclosing what seems to be a finite area.