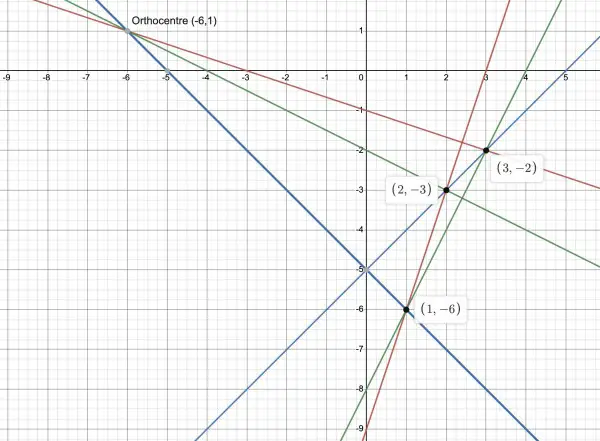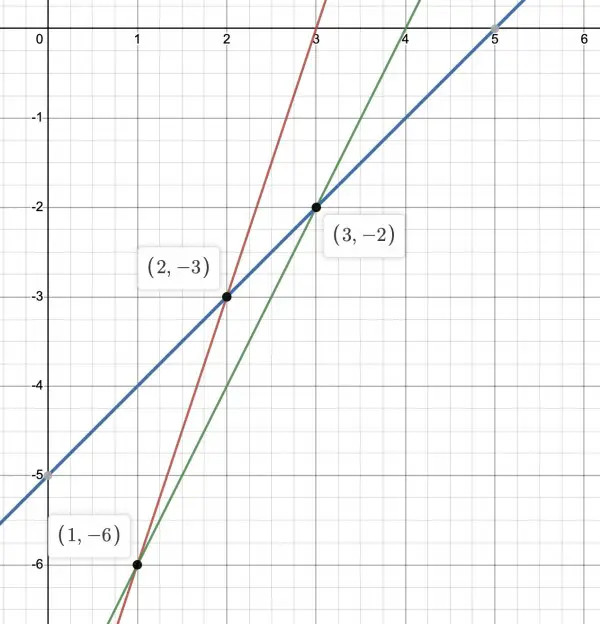
3x-y=9, x-y=5, 2x-y=8 are shown on the graph with their intersection points.
Red and blue intersect when y=3x-9=x-5, 2x=4, x=2 and y=-3; blue and green intersect when y=x-5=2x-8, x=3 and y=-2; and red and green intersect when y=3x-9=2x-8, x=1 and y=-6.
The points (2,-3), (3,-2) and (1,-6) form the vertices of a triangle. The orthocentre is the intersection of the three altitudes, that is, the perpendiculars from the vertices on to the opposite sides.
Only two perpendiculars are needed to find the orthocentre. The slope of the red line is 3 so the slope of its perpendicular is -⅓, and this has to pass through (3,-2) to produce the perpendicular to vertex (3,-2). The equation of the line is y+2=-⅓(x-3), y=-x/3-1. The slope of the blue line is 1 so the slope of the perpendicular is -1, passing through (1,-6) produces the equation y+6=-(x-1), y=-x-5. So the intersection of these perpendiculars is when y=-x/3-1=-x-5, x/3+1=x+5, ⅔x=-4, x=-6 and y=1, the point (-6,1).
Just to make sure, use the slope of green, which is 2, so its perpendicular has slope -½, equation y+3=-½(x-2), y=-x/2-2. This should pass through (-6,1), which it does, confirming the orthocentre (-6,1).