Assuming the circle lies in the x-y plane (z=0), then the given plane intersects the x-y plane when 2x+3y=1.
The equation of the circle in general form is:
(x-h)2+(y-k)2=r2, where (h,k) is the centre and r is the radius. The centre lies on the line 2x+3y=1 so the point (h,k) must satisfy: 2h+3k=1.
Plug the given points into the general equation:
(2-h)2+k2=r2, (1+h)2+(4-k)2=r2,
(2-h)2+k2=(1+h)2+(4-k)2,
4-4h+h2+k2=1+2h+h2+16-8k+k2,
6h-8k=-13,
2h+3k=1, 6h+9k=3,
17k=16, k=16/17, so 2h+48/17=1, 2h=-31/17, h=-31/34.
r2=(2+31/34)2+256/289=9801/1156+1024/1156=10825/1156.
The equation of the circle is (x+31/34)2+(y-16/17)2=10825/1156.
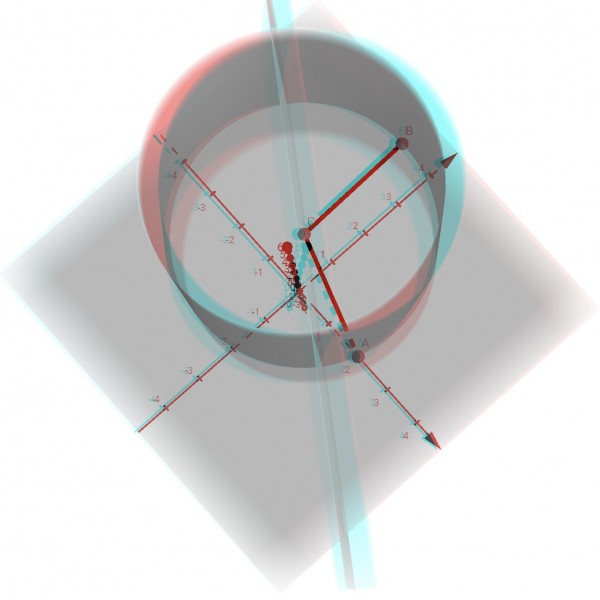
The image below represents the circle as a vertical cylinder. The thin line is a view from almost directly above showing that the intersection of the given plane with the x-y plane (grey area) is a diameter of the circle centre C(-31/34,16/17) and passing through A(2,0) and B(-1,4). Radii CA and CB have been drawn for clarity. The z-axis is vertical (pointing out of the page. The image is best viewed using 3D lenses (green/blue filter right, red filter left). The circle (cross-section of the cylinder) lies on the x-y plane.