Surveyor is measuring the length of a lake

Question

A surveyor is is measuring the length of a lake. he takes angle measurements from two positions A and B, that are 550 m apart, and on opposite sides of the lake. From B, the Measure of the angle between the sight lines to the ends of the lake is 130', and the measure of the angle wetewwn the sight lines to A and one end of the lake is 110'. from A the measure of the angle btween the sight lines to the ends of the lake is 77', and the lenght of the measure of the angle tweteen the sight lines to B and the same end of the lake is 22'. Calculate the lenth of the lake , to the nearest metre. show your work.

Answer 1

CONSTRUCTION 

Draw line AB (representative length 550m). 

The two endpoints of the lake we can call P and Q. 

At point B make an angle of 110° (towards P) on one side of AB and 20° (towards Q) on the other side of AB. This will create an angle PB̂Q=130°. 

At point A make an angle of 22° (angle BÂP) towards P and 55° (angle BÂQ) towards Q. This will create an angle PÂQ=77°.

This construction creates a quadrilateral AQBP. AQ̂B=180-(20+55)=105° and AP̂B=180-(110+22)=48°.

To find PQ, the length of the lake, we need to find two sides, QB and BP, or QA and AP. We have all the angles in AQBP so we can use the Sine Rule to find the lengths of one of these pairs.

In triangle ABP, AB/sinAP̂B=BP/sinBÂP, 550/sin(48)=BP/sin(22), BP=550sin(22)/sin(48)=227.25m approx. In triangle ABQ, AB/sinAQ̂B=QB/sinBÂQ, 550/sin(105)=QB/sin(55), QB=550sin(55)/sin(105)=466.43m approx.

Now the Cosine Rule can be applied to triangle PQB:

PQ²=QB²+BP²-2QB.BPcosPB̂Q=466.43²+227.25²-2×466.43×227.25cos(130),

PQ²=460663 approx, PQ=678.72m, which is the length of the lake.

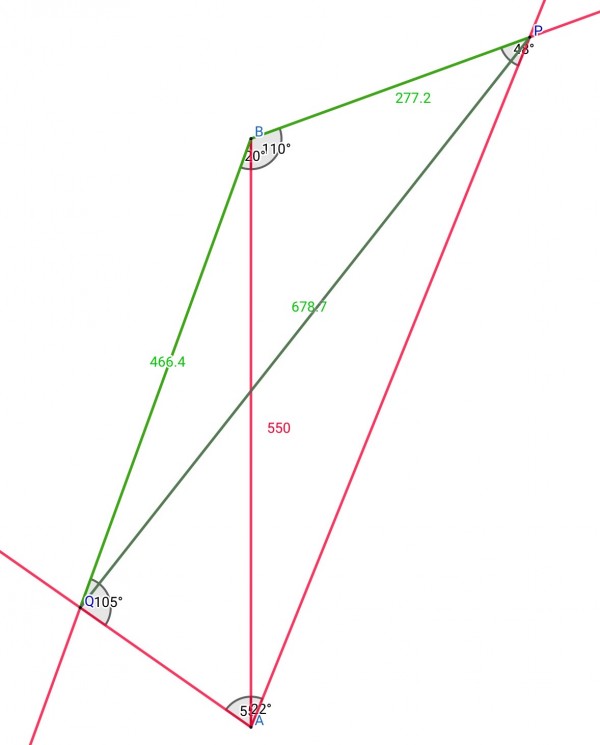
The extended red rays from A and B represent the line of sight measurements by the surveyor. It's the intersections of these lines of sight that fix the positions of the endpoints P and Q of the lake. The large angle at A is 77°, but is shown as 55°+22° in the picture. Similarly the large angle at B is 130°, split into 110°+20°. The green measurements are the results of calculation in the solution. The picture is to scale.