The first thing to note is that no minimum percentage has been given for the most expensive ingredient C, which implies that the minimum is 0%.
The minimum quantity of mixture is 12kg. The maximum quantity M is calculated from the limited supply of ingredient A, which must be at least 45% of the mixture, that is, 0.45M=10kg, and M=10/0.45=200/9kg. So we can write: 12≤A+B+C≤200/9 kg. In the graph below, X=A+B+C, the sum of the quantities of the ingredients.
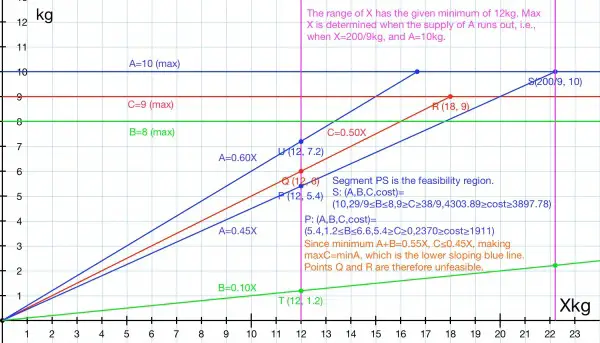
When the mixture weighs 12kg, 5.4kg (45%) of it will be A. That leaves 6.6kg for the remaining ingredients: 1.2≤B≤6.6 and 5.4≥C≥0 because B+C=6.6kg. The cost of 12kg can be calculated: (A,B,C)={(5.4,1.2,5.4)...(5.4,6.6,0)} giving us a range for cost={ 2370...1911 }. Therefore, the range of costs for a 12kg mixture is [1911,2370]. The unit cost has a range of [159.12,197.5] per kg.
When the mixture weighs 200/9kg, the whole 10kg supply of A is used up. This time B+C=200/9-10=110/9kg. The picture below illustrates how the feasibility region (thick black line segment) is found.
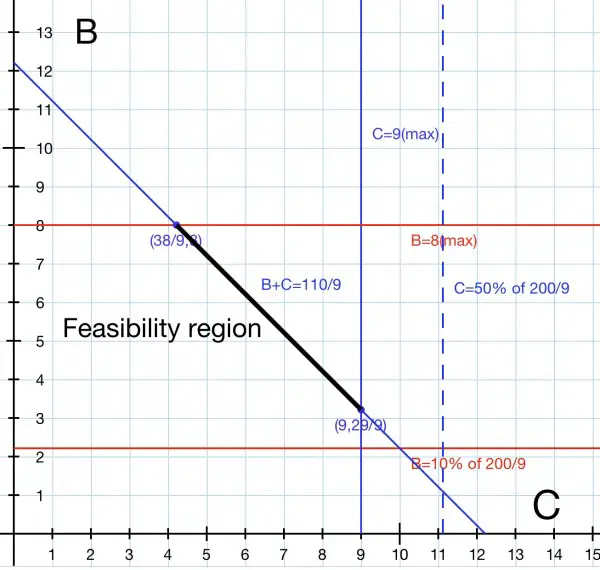
Note that maxC (50% of the mixture, C=100/9kg), indicated by the broken blue vertical line, is actually greater than the 9kg supply for C, so it is superseded by the constraint.
The range for (A,B,C) involves the complete 8kg supply of B, leaving 38/9kg for C; and the complete 9kg supply of C, leaving 29/9kg for B: (A,B,C)={(10,8,38/9)...(10,29/9,9)} giving a cost range [3897.8,4303.9]. The unit cost range is [175.4,198.675].
So it’s clear that the 12kg mixture gives the minimum unit rate and production cost: 159.12/kg and 1911, made from 5.4kg of A and 6.6kg of B, no C.