mid point theorem

Question

show that the line segments joining mid points of the opposite sides of a quadrileteral bisect each other

Answer 1

 

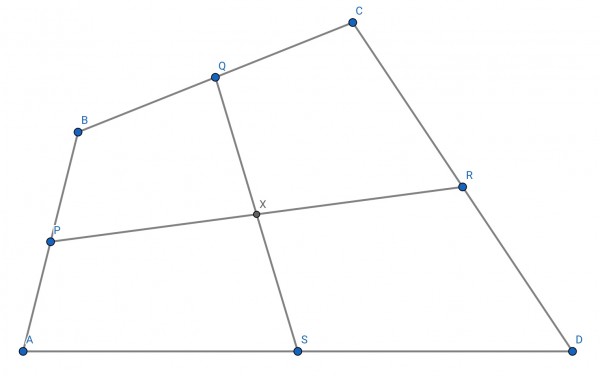
This can be proved graphically.

A(0,0), B(b₁,b₂), C(c₁,c₂), D(d₁,0) form a quadrilateral ABCD.

The midpoint of a line has the average of the coordinates of its endpoints.

The midpoint of AB is P(b₁/2,b₂/2),

midpoint of BC is Q((b₁+c₁)/2,(b₂+c₂)/2),

midpoint of CD is R((c₁+d₁)/2,c₂/2),

midpoint of AD is S(d₁/2,0),

midpoint of PR is X((b₁+c₁+d₁)/4,(b₂+c₂)/4),

midpoint of QS is X((b₁+c₁+d₁)/4,(b₂+c₂)/4).

So the midpoint of PR and QS is the same (point X), therefore the line joining the midpoints of opposite sides of a quadrilateral bisect one another.