Right spherical triangle C=90°. a, b, c are sides (measured as arc (subtended) angles of great circles) and triangle angles A, B , C as in plane triangles.
Note that in any triangle (spherical or plane) the shortest side is opposite the smallest angle. Also, the ratio of the sides in a triangle is the same as the ratio of the sines of their opposite angles (Sine Rule). These rules do not seem to be apparent in this question, but proof can be seen below in the application of Napier's Rule.
Napier’s Pentagon consists of 5 pentagon triangles p₁-p₅ inside a circle. The order of sides and angles (clockwise) is pentagon triangles containing b, A, c, B, a, cyclically reordered as a, b, A, c, B, so that:
p₁=a, p₂=b, p₃=A, p₄=c, p₅=B. For p₃-p₅ complement the angles so we get: a, b, 90-A, 90-c, 90-B. Napier’s Pentagon helps to derive equations.
For a the adjacent pentagon triangles are b and 90-B and the opposite triangles are 90-A and 90-c. For b the adjacent triangles are a and A and the opposite triangles are B and c.
Napier’s Rules:
(1) sin(a)=cos(90-A)cos(90-c) (SIN-CO-OP); (2) sin(a)=tan(b)tan(90-B) (SIN-TA-AD);
(1) sin(b)=cos(90-c)cos(90-B); (2) sin(b)=tan(90-A)tan(a), etc. SIN-CO-OP and SIN-TA-AD are the mnemonic representations; the relevant trig function can replace the trig function of complements (sin becomes cos and tan becomes cot).
In all, 10 equations can be derived by starting with any pentagon triangle. The sine of the “middle” triangle (which has two opposite and two adjacent triangles) can be derived from its adjacent (tangent product) and opposite (cosine product) pentagon triangles.
Unfortunately, in this question, B is defined as two different angles, and we don't have the size of angle A. So we have to assume that one of the given angles is A and the other B, but which is which? We need to explore the possibilities.
Here is Napier's Pentagon
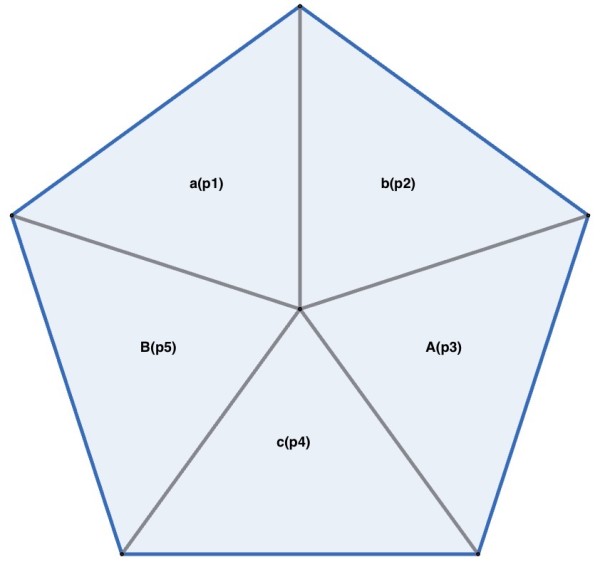
Decimals are to 6 decimal place accuracy, and angles to the nearest minute.
(1) sin(a)=cos(90-A)cos(90-c)=sin(A)sin(c)=tan(b)tan(90-B)=tan(b)cot(B);
sin(a)=sin(14°24')=0.248690, cos(a)=0.968583 (because we are given a);
(2) sin(b)=cos(90-c)cos(90-B)=sin(c)sin(B)=tan(90-A)tan(a)=cot(A)tan(a);
sin(b)=sin(147°15')=0.540974, cos(b)=-0.841039 (because we are given b);
(3) sin(90-c)=cos(c)=cos(a)cos(b)=tan(90-A)tan(90-B)=cot(A)cot(B).
In (3) the ambiguity between A and B is irrelevant, because of the tangent product involving both angles.
sin(90-c)=cos(c)=tan(90-A)tan(90-B)=tan(-34°15')tan(-40°30')=0.581523,
c=cos-1(0.581523)=54°27'.
Since cos(c)=0.581523=cos(a)cos(b)=tan(90-A)tan(90-B)=cot(A)cot(B) and we know a and b we can confirm (or invalidate) (3).
cos(a)cos(b)=0.968583(-0.841039)=-0.814616.
So we have an inconsistency, because cos(c)=0.581523 but cos(a)cos(b)=-0.814616, and cos(c)≠sin(a)sin(b).
GIven this apparent inconsistency, it's not possible to proceed.
The Sine Rule (which applies to plane and spherical triangles) also fails to be true no matter which angle is A or B.