Draw the sine graph w/ step-by-step solution.

Question

Draw the graph of:

1.)   -2 sin ( 2x + 3pi ) + 2

Answer 1

Let's look at and compare sin(2x) and sin(2x+3π).

sin(2x+3π)=sin(2x)cos(3π)+cos(2x)sin(3π). Since sin(3π)=0 and cos(3π)=-1, sin(2x+3π)=-sin(2x).

Therefore -2sin(2x+3π)=-(-2sin(2x))=2sin(2x).

Now compare sin(2x) with sin(x). When x=π/2 (90°), sin(x)=1; when x=π/4 (45°), sin(2x)=1. So the graph of sin(2x) looks like sin(x) compressed so that there are two cycles of sin(2x) for every cycle of sin(x).

2sin(2x) has twice the amplitude of sin(2x), which means that the peaks are twice as high and the troughs twice as deep.

Finally adding 2 to the function shifts the whole sine wave up two units so that it sits on the x-axis.

These are the steps:

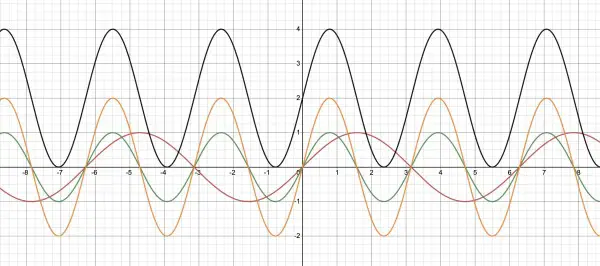
1. The parent function is y=sin(x) (in red) which starts at (0,0) and rises to its peak at (π/2,1), falls to intersect the x-axis at (π,0), drops to its trough at (3π/2,-1) and then rises to intersect the x-axis at (2π,0). This pattern is repeated all the way along the x-axis (positive and negative).
2. y=sin(2x) (green) looks similar but more compressed than y=sin(x), starting at (0,0), peaks at (π/4,1), intersects the x-axis at (π/2,0), trough at (¾π,-1) and intersects again at (π,0). So two cycles of y=sin(2x) fit into one of y=sin(x).
3. y=2sin(2x) (orange) rises to (π/4,2), twice as high as y=sin(2x), and its trough is at (¾π,-2), twice as deep as y=sin(2x); but it intersects the x-axis at the same points as y=sin(2x).
4. As explained earlier, y=-2sin(2x+3π) is the same as y=2sin(2x).
5. y=-2sin(2x+3π)+2=2sin(2x)+2 (black), which lifts up y=2sin(2x) 2 units, so its peak is at (π/4,4) and trough at (¾π,0) (on the x-axis).

π=3.14, ½π=1.57, ¼π=0.79, ¾π=2.36, 2π=6.28 approx.