find equation of tangent of parameric equ x=t-2sint, y=2-2cost at t=π/4

Question

Consider the parametric equations

x=t-2sin(t), y=2-2cos(t)

a) determine an equation of the tangent line when t=π/4

b) Determine the stationary point(s) of the curve.

Answer 1

dy/dt=(dy/dx)(dx/dt), so tangent=dy/dx=(dy/dt)/(dx/dt).

dy/dt=2sin(t), dx/dt=1-2cos(t), dy/dx=2sin(t)/(1-2cos(t)).

At t=π/4, sin(t)=cos(t)=½√2.

dy/dx|_t=π/4=√2/(1-√2)=√2(1+√2)/(1-2)=-√2(1+√2)=-2-√2.

(a) The tangent at t=π/4 is -2-√2.

Let m=-2-√2. At t=π/4, x=t-2sin(t)=π/4-√2, y=2-2cos(t)=2-√2.

The equation of the tangent line is y-2+√2=-(2+√2)(x-π/4+√2),

y=-(2+√2)x+¼π(2+√2)-3√2.

(b) dy/dx=2sin(t)/(1-2cos(t))=0 at the stationary points.

sin(t)=0 when t=nπ where n is an integer. cos(nπ)=-1 when n is odd (2m+1) and 0 when n is even (2m).

So the stationary points occur when:

x=t-2sin(t)=πn,

y=2-2cos(t)=2-2cos((2m+1)π)=2+2=4 and y=2-2cos(2mπ)=2-2=0.

When n=0, t=0, (0,0); n=1, t=π, (π,4); n=2, t=2π, (2π,0); n=3, t=3π, (3π,4); n=4, t=4π, (4π,0); ...

The stationary points appear to be:

{..., (-4π,0), (-3π,4), (-2π,0), (-π,4), (0,0), (π,4), (2π,0), (3π,4), (4π,0), ...}

However, we can write x in terms of y:

x=arccos(1-½y)-2√(y-¼y²) which only exists when y-¼y²≥0, y(1-¼y)≥0 and -1≤1-½y≤1, that is, 0≤y≤4.

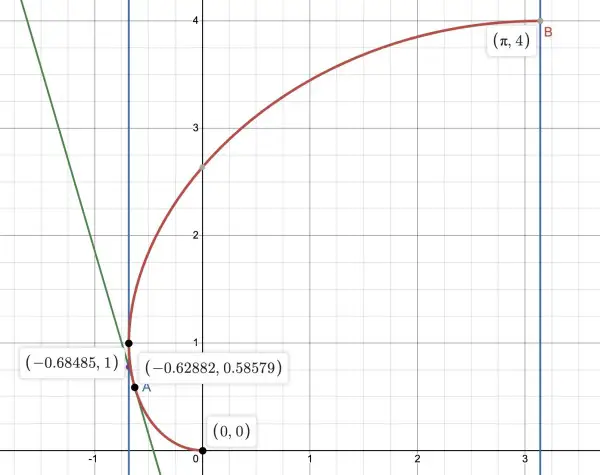
So there are only two stationary points: (0,0) and (π,4). When y=4, x=arccos(-1)=π.

Note also that (π/3-√3,1) is the leftmost point on the graph so π/3-√3≤x≤π.

The red curve is the graph of x=arccos(1-½y)-2√(y-¼y²). The stationary points are shown as the origin (0,0) and the point B(π,4), the rightmost point on the curve.

Point A is the point corresponding to t=π/4 and the green line is the tangent line at A. The left vertical blue line marks the lowest value of x and the leftmost point on the curve (π/3-√3,1), corresponding to t=π/3.

The y-intercept corresponds to t=1.8955 approx and the point (0,2.638) approx. (t is one solution of sin(t)=½t, the other solution being t=0 at the origin.)